演算法 - 選擇排序法 (Selection Sort)
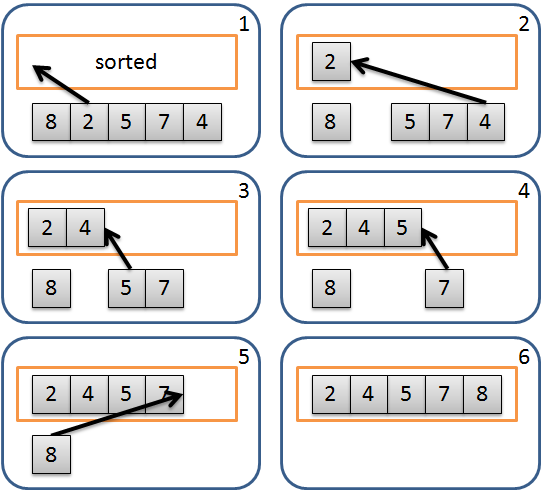
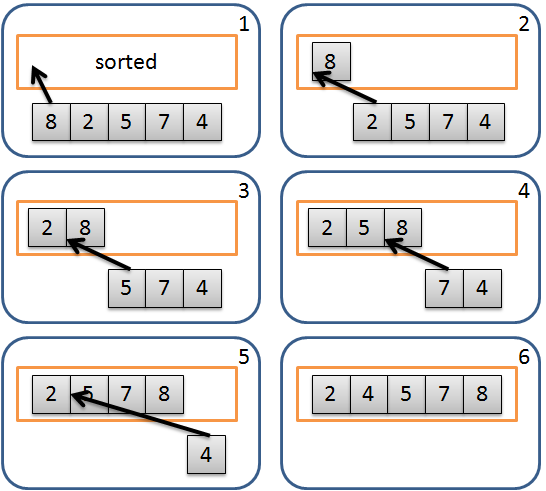
簡介選擇排序法 (Selection Sort) 是排序演算法的一種,也是一種簡單容易理解的演算法,其概念是反覆從未排序的數列中取出最小的元素,加入到另一個的數列,結果即為已排序的數列。運算流程如下: 從未排序的數列中找到最小的元素。 將此元素取出並加入到已排序數列最後。 重複以上動作直到未排序數列全部處理完成。 流程示意圖: 然而實作上通常不使用額外的數列來儲存已排序的部分,而使用原地 (In-place) 的方式來完成,數列的左半部表示已排序部分,右半部表示未排序部分,不另外使用數列。從未排序部分找到最小的元素,利用交換的方式將元素放置已排序部分的尾端。運算流程如下: 從未排序的數列中找到最小的元素。 將此元素與已排序部分的尾端元素進行交換。 重複以上動作直到未排序數列全部處理完成。 流程示意圖: 選擇排序法的比較複雜度固定是 O(n^2),不過交換次數則是 O(n),在最佳情況可以到 O(0),比起氣泡排序法的比較次數少很多,所以效能上會比較好。 分析 最佳時間複雜度:O(n^2) 平均時間複雜度:O(n^2) 最差時間複雜度:O(n^2) 空間複雜度:O(1) Stab ...
演算法 - 插入排序法 (Insertion Sort)
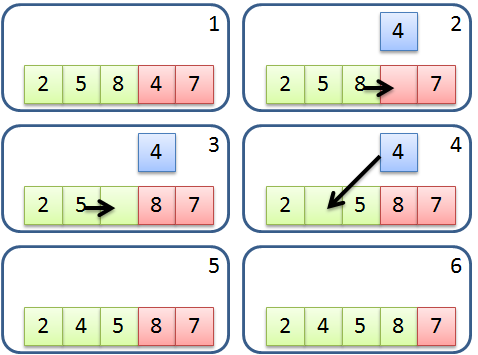
簡介插入排序法 (Insertion Sort) 是排序演算法的一種,他是一種簡單容易理解的排序演算法,其概念是利用另一個數列來存放已排序部分,逐一取出未排序數列中元素,從已排序數列由後往前找到適當的位置插入。運算流程如下: 從未排序數列取出一元素。 由後往前和已排序數列元素比較,直到遇到不大於自己的元素並插入此元素之後;若都沒有則插入在最前面。 重複以上動作直到未排序數列全部處理完成。 流程示意圖: 然而實作上通常不使用額外的數列來儲存已排序的部分,而使用原地 (In-place) 的方式來完成,數列的左半部表示已排序部分,右半部表示未排序部分,不另外使用數列。在與已排序的部分比較時,利用指派 (Assign) 的方式將元素往右位移,來達到插入的效果,因為位移的關係需要有另一個變數來暫存最右邊的數值。運算流程如下: 將未排序的部分最左邊元素儲存到暫存變數。 由後往前和已排序部分元素比較,若比自己大則將該元素往右邊位移。 重複2的動作直到遇到不大於自己的元素,將暫存變數寫入在該元素之後;若都沒有則寫入在最前面。 重複以上動作直到未排序部分全部處理完成。 流程示意圖: 分析 最佳 ...
演算法 - 氣泡排序法 (Bubble Sort)
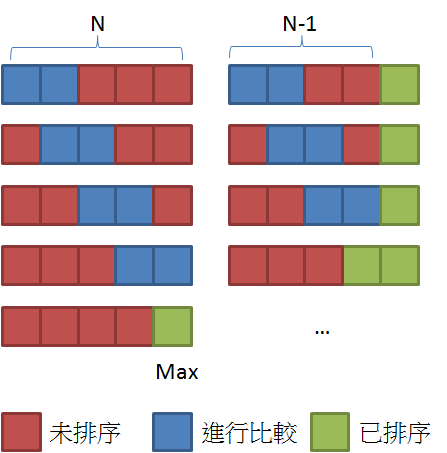
簡介氣泡排序法 (Bubble Sort) 是最容易理解和實作的一種排序演算法,也翻譯作冒泡排序法。由於它很容易學習,所以也是許多演算法課程中第一個學習的排序演算法。 由於他的演算法過程會將最大的數值移動到陣列最後面,而較小的數值則逐漸的往陣列前端移動,就像有許多氣泡慢慢從底部浮出,因此稱為氣泡排序法。他的運作流程如下: 比較相鄰的兩個元素,若前面的元素較大就進行交換。 重複進行 1 的動作直到最後面,最後一個元素將會是最大值。 重複進行 1, 2 的動作,每次比較到上一輪的最後一個元素。 重複進行以上動作直到沒有元素需要比較。 流程示意圖: 實作上直接使用迴圈就可以很容易的完成。另外可以使用額外的旗標 (Flag) 來判斷這一輪是否有發生交換情形,若都沒有發生交換表示數列已經是排序好的,即可跳出迴圈,因此最佳時間複雜度是有可能達到 O(n)。 分析 最佳時間複雜度:O(n) 平均時間複雜度:O(n^2) 最差時間複雜度:O(n^2) 空間複雜度:O(1) Stable sort:是 虛擬碼一般版本1234567891011function sort(list) // 重複 N ...
排序演算法 (Sorting)
簡介排序 (Sorting) 演算法是常用到的一種演算法,顧名思義他是用來將資料依據特定的規則做排序後輸出;既然稱為排序就會有一個比較順序的依據,例如數字就比較數值大小、字串則依 ASCII 字母順序或者物件會有自定義的規則。一般沒有特別指定的話,輸出是以遞增排序為準。 穩定排序排序演算法分為穩定 (Stable) 和不穩定 (Unstable) 兩種,是指當資料中有相等數值的兩元素,經過排序之後是否能夠保持原有的相對位置,例如: 1(猴子, 智商60) (丁丁, 智商20) (拉拉, 智商20) (路人甲, 智商90) 將這些資料依據智商來排序,會發現智商 20 的有兩位,因此我們可能得到以下兩種情況 12(丁丁, 智商20) (拉拉, 智商20) (猴子, 智商60) (路人甲, 智商90)(拉拉, 智商20) (丁丁, 智商20) (猴子, 智商60) (路人甲, 智商90) 第一種情況丁丁和拉拉與原始的相對位置一致 (丁丁在前),能夠總是維持相對位置的排序法我們稱之為穩定排序,反之則稱為不穩定排序,不能確保相對位置與原來一樣 (但是也有可能一樣)。 如果是純數字的排序基本上是 ...
演算法 - 快速排序法 (Quick Sort)
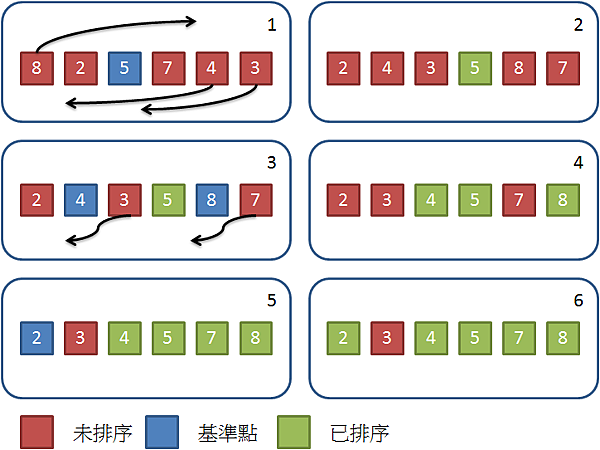
簡介快速排序法是排序演算法的一種,使用 Divide and Conquer 的演算法來實作。其概念是從數列中挑選一個基準點,大於基準的放一邊,小於的放一邊,如此循環最後可完成排序。過程依照以下步驟進行(遞增為例): 數列中選擇一元素作為基準點 (pivot)。 小於此元素的移至基準的左邊,大於此元素的移至右邊,相等的任意放。 基準點左邊和右邊視為兩個數列,並重複做以上動作直到數列剩下一個或零個元素。 流程範例如圖所示: 實作的方式除了一般使用額外的暫存數列之外,也有使用較少額外空間的 原地 (In-place) 方式,In-place 的方式主要概念是將基準點暫時移到最右邊,小於基準的移至數列一端並記錄遞增索引,最後將基準點換回索引位置,過程依照以下步驟進行 (遞增為例): 數列中選擇一元素作為基準點 (pivot),並與最右邊的元素交換位置。 建立一索引指向最左邊元素。 小於基準的元素與索引位置的元素交換位置,每次交換後遞增索引。 完成後將基準點與索引位置的元素交換位置。 基準點左邊和右邊視為兩個數列,並重複做以上動作直到數列剩下一個或零個元素。 流程範例如圖所示: 基準點 ...
演算法 - 合併排序法 (Merge Sort)
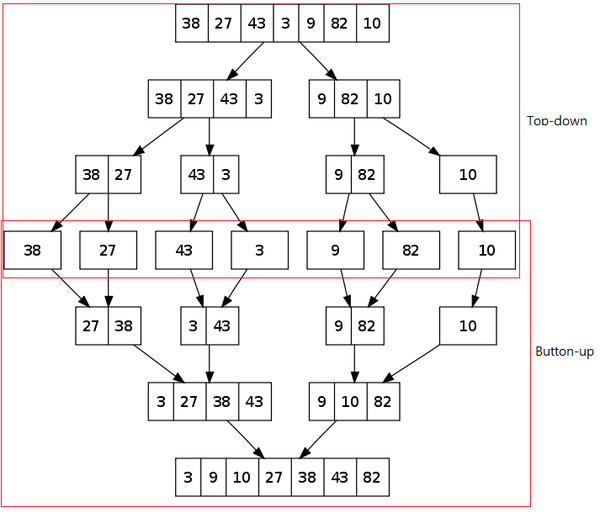
簡介合併排序法 (或稱歸併排序法),是排序演算法的一種,使用 Divide and Conquer 的演算法來實作。排序時需要額外的空間來處理,過程依照以下步驟進行: 將陣列分割直到只有一個元素。 開始兩兩合併,每次合併同時進行排序,合併出排序過的陣列。 重複2的動作直到全部合併完成。 流程範例如圖所示: 實作又可分為 Top-down 和 Bottom-up,依據原始的步驟會先將陣量分割直到剩一個元素 (Top-down),然而也可以一開始就直接切割成單一元素開始合併 (Bottom-up)。 分析 最佳時間複雜度:O(nlog n) 平均時間複雜度:O(nlog n) 最差時間複雜度:O(nlog n) 空間複雜度:O(n) Stable sort:是 虛擬碼以下以較高階的想法寫出虛擬碼,實作上效能要好必須還要進一步修改: Top-down12345678910111213141516171819202122function sort(list) if list.length == 1 return list end if left = 取出從 list[0] 到 list ...