資料結構 - 一般樹轉二元樹

簡介

在樹狀結構中我們可能會使用陣列或指標來表示子節點，然而許多的陣列或指標並沒有真的利用到，造成記憶體上的浪費。透過特定的儲存方式，能夠將各種樹都轉換成二元樹，就能有效解決這個問題。轉換的規則如下：

原節點的第一個子節點轉成二元樹中的左子節點。
原節點的下一個兄弟節點轉成二元樹中的右子節點。

從圖形的角度來看也可以這樣說：

原節點的第一個指標指向第一個子節點。
原節點的第二個指標指向下一個兄弟節點。

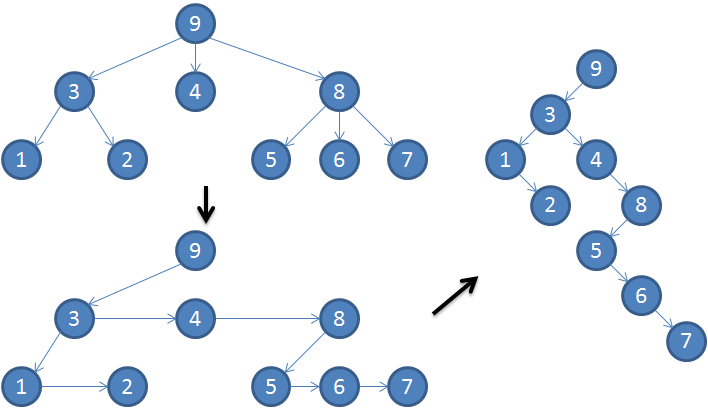
轉換過程以下面這張圖為例：

左上角的圖表示原來的一般樹，從圖形的角度並以節點3為例，透過規則1將節點3的第一個指標指向第一個子節點，第一個節點我們簡單取最左邊的節點，為節點 1；透過規則 2 將節點 3 的第二個指標指向下一個兄弟節點，為節點 4。

其他以此類推，接著我們可以得到左下角的圖形，與原來的規則做對應我們可以知道，第一個指標指的就是二元樹的左子節點，第二個指標就是右子節點，所以依據左右子節點的位置重新調整圖形，最後可以得到右邊的徒刑，也就是轉換成二元樹的結果。

LCRS Tree

從上面的轉換結果，我們可以知道這個二元樹的左子節點代表的是原來的第一個子節點，右子節點代表下一個兄弟節點，而這樣的性質的樹也稱為 LCRS Tree(Left-Child-Right-Sibling Tree)。

原始的樹如果在後序 (Post-order) 的情況為排序好的，再轉換為二元樹後，也同時會是一個二元搜索樹。

語法

這邊利用之前文章寫過的樹和二元樹程式來做轉換。

C#

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using BinaryTree;
using Tree;

namespace LcrsTree
{
    public class LcrsTree
    {
        static public BinaryTree<T> Convert<T>(Tree<T> tree)
        {
            BinaryTree<T> binaryTree = new LinkedBinaryTree<T>(tree.Value);
            IEnumerator<Tree<T>> enu = tree.Children.GetEnumerator();
            if (enu.MoveNext())
            {
                binaryTree.AddLeft(Convert(enu.Current));
                BinaryTree<T> node = binaryTree.Left;
                while (enu.MoveNext())
                {
                    node.AddRight(Convert(enu.Current));
                    node = node.Right;
                }
            }
            return binaryTree;
        }
    }
}

Java

import java.util.Iterator;


public class LcrsTree {

    static public <T> BinaryTree<T> convert(Tree<T> tree) throws Exception
    {
        BinaryTree<T> binaryTree = new LinkedBinaryTree<T>(tree.getValue());
        Iterator<Tree<T>> iterator = tree.children().iterator();
        if (iterator.hasNext())
        {
            binaryTree.addLeft(convert(iterator.next()));
            BinaryTree<T> node = binaryTree.left();
            while (iterator.hasNext())
            {
                node.addRight(convert(iterator.next()));
                node = node.right();
            }
        }
        return binaryTree;
    }
}

C++

#ifndef LCRSTREE_H
#define LCRSTREE_H

template<typename T>
class LcrsTree
{
    public:
        LcrsTree() {}
        virtual ~LcrsTree() {}

        static BinaryTree<T>* convert(Tree<T>* tree)
        {
            BinaryTree<T>* binaryTree = new LinkedBinaryTree<T>(tree->getValue());
            TreeList<string>* children = tree->children();
            children->begin();
            if(Tree<T>* child = children->next())
            {
                binaryTree->addLeft(convert(child));
                BinaryTree<T>* node = binaryTree->left();
                while (child = children->next())
                {
                    node->addRight(convert(child));
                    node = node->right();
                }
            }
            return binaryTree;
        }
    protected:
    private:
};

#endif // LCRSTREE_H