演算法 - 二元搜索法 (Binary Search)

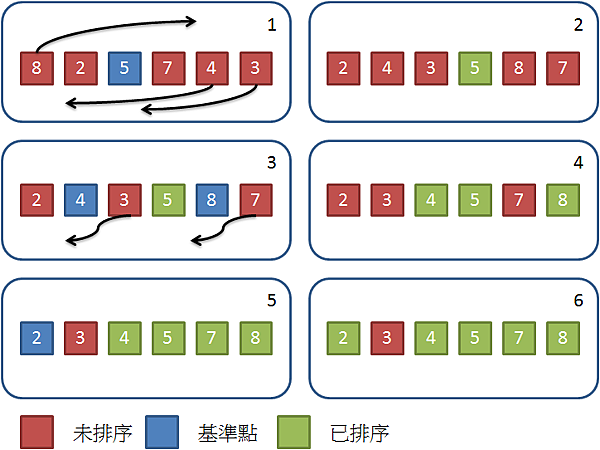
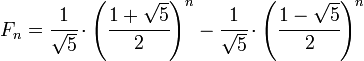簡介

二元搜索法 (Binary Search) 又稱折半搜索，搜索演算法的一種，可使用 Divide and Conquer 或直接使用迴圈 (迭代) 來實作，搜索的目標資料必須是已經排序過的 (以小到大排序為例)。其概念是每次挑選中間位置的資料來比對，若該資料小於目標值，則縮小範圍為左半部，反之亦然；因此使用這個方法每次比對後都可以濾掉一半的資料，以增快搜索速度。過程依以下步驟進行：

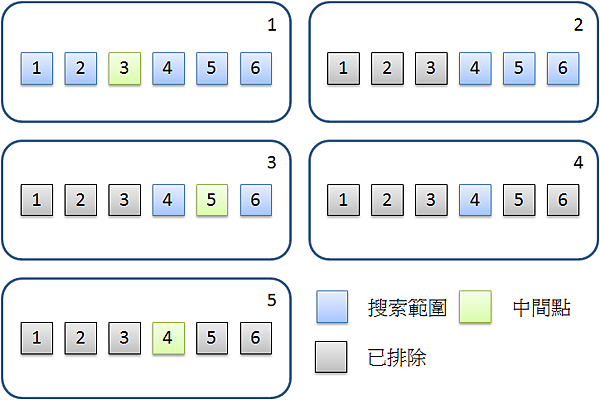
取出搜索範圍中點的元素。
與搜索目標比較，若相等則回傳位址。若小於則將左邊邊界改為中點右側，若大於則將右邊邊界改為中點左側。
左邊邊界不超過右邊邊界(還有資料)則重複以上動作，若已無資料則回傳-1(找不到)。

流程範例如圖所示，例如搜索值為4的元素：

分析

最佳時間複雜度：O(1)
平均時間複雜度：O(log n)
最差時間複雜度：O(log n)
空間複雜度：O(1)

虛擬碼

迭代

function search(list, target)
	var left = 0, right = list.length - 1
	while left <= right
		var middle = 取出 list 中點
		if list[middle] == target
			return middle
		// 比目標大，再搜索左半邊
		else if list[middle] > target
			right = middle - 1
		// 比目標小，再搜索右半邊
		else if list[middle] < target
			left = middle + 1
		end if
	end while
	return -1
end function

Divide and Conquer

function search(list, target, left, right)
	if left > right
		return -1
	end
	var middle = 取出 list 中點
	if list[middle] == target
		return middle
	// 比目標大，再搜索左半邊
	else if list[middle] > target
		return search(list, target, left, middle - 1)
	// 比目標小，再搜索右半邊
	else if list[middle] < target
		return search(list, target, middle + 1, right)
	end if
	return
end function

語法

C#

迭代

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace BinarySearch
{
    class Iterative
    {
        static public int Search(int[] array, int num)
        {
            int left = 0, right = array.Length - 1;
            while (left <= right)
            {
                int middle = (right + left) / 2;

                if (array[middle] == num)
                    return middle;

                if (array[middle] > num)
                    right = middle - 1;
                else
                    left = middle + 1;
            }
            return -1;
        }
    }
}

Divide and Conquer

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace BinarySearch
{
    class DivideAndConquer
    {
        static public int Search(int[] array, int num)
        {
            return Search(array, num, 0, array.Length - 1);
        }

        static public int Search(int[] array, int num, int left, int right)
        {
            if (left > right)
                return -1;

            int middle = (right + left) / 2;

            if (array[middle] == num)
                return middle;

            if (array[middle] > num)
                return Search(array, num, left, middle - 1);

            return Search(array, num, middle + 1, right);
        }
    }
}

Java

迭代

public class Iterative {
    static public int Search(int[] array, int num)
    {
        int left = 0, right = array.length - 1;
        while (left <= right)
        {
            int middle = (right + left) / 2;

            if (array[middle] == num)
                return middle;

            if (array[middle] > num)
                right = middle - 1;
            else
                left = middle + 1;
        }
        return -1;
    }
}

Divide and Conquer

public class DivideAndConquer {
    static public int Search(int[] array, int num)
    {
        return Search(array, num, 0, array.length - 1);
    }

    static public int Search(int[] array, int num, int left, int right)
    {
        if (left > right)
            return -1;

        int middle = (right + left) / 2;

        if (array[middle] == num)
            return middle;

        if (array[middle] > num)
            return Search(array, num, left, middle - 1);

        return Search(array, num, middle + 1, right);
    }
}

C++

迭代

Iterative.h

#ifndef ITERATIVE_H
#define ITERATIVE_H

class Iterative
{
    public:
        static int Search(int* array, int length, int num);
    protected:
    private:
};

#endif // ITERATIVE_H

Iterative.cpp

#include "Iterative.h"

int Iterative::Search(int* array, int length, int num)
{
    int left = 0, right = length - 1;
    while (left <= right)
    {
        int middle = (right + left) / 2;

        if (array[middle] == num)
            return middle;

        if (array[middle] > num)
            right = middle - 1;
        else
            left = middle + 1;
    }
    return -1;
}

Divide and Conquer

DivideAndConquer.h

#ifndef DIVIDEANDCONQUER_H
#define DIVIDEANDCONQUER_H

class DivideAndConquer
{
    public:
        static int Search(int* array, int length, int num);
        static int Search(int* array, int num, int left, int right);
    protected:
    private:
};

#endif // DIVIDEANDCONQUER_H

DivideAndConquer.cpp

#include "DivideAndConquer.h"

int DivideAndConquer::Search(int* array, int length, int num)
{
    return Search(array, num, 0, length - 1);
}

int DivideAndConquer::Search(int* array, int num, int left, int right)
{
    if (left > right)
        return -1;

    int middle = (right + left) / 2;

    if (array[middle] == num)
        return middle;

    if (array[middle] > num)
        return Search(array, num, left, middle - 1);

    return Search(array, num, middle + 1, right);
}

產生1-100000之陣列，並搜索1-100000實測

C#
Iterative: 30ms - 40ms
DivideAndConquer: 60ms - 70ms

Java
Iterative: 10ms - 20ms
DivideAndConquer: 20ms - 30ms

C++
Iterative: 10ms - 30ms
DivideAndConquer: 20ms - 30ms