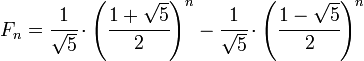程式技術

常見考題包含了基礎的演算法和資料結構，以及一些其他類型的程式實作考題。 演算法 分治法 (Divide and conquer) 二元搜索法 (Binary Search) 動態規劃 (Dynamic Programming) 費波那西數列 (Fibonacci) 上下樓梯問題 & (籃球) 得分問題 最大子序列 (Maximum Subarray) 排序演算法 (Sorting) 資料結構 連結串列 (LinkedList) 堆疊 (Stack) 佇列 (Queue) 其他考古題 不使用暫存變數交換兩個變數 (Swap two variables without using a temporary variable) 計算 1 + 2 + 3 + … + N 的總和 (Sum the Integers from 1 to N)可以思考不同的解法，例如： 使用遞迴 比 O(n) 時間複雜度更快的方法 計算1 * 2 + 2 * 3 + … + (N - 1) * N的總和 (Write a function to calculate 1 * 2 + 2 * 3 ...

題目未排序的 n 個連續整數中少了一個，試著找到最快的方法算出少了哪一個。例如：3, 6, 9, 7, 8, 4，連續整數範圍為 3-9，少了 5。How to find the missing integer in an array. 說明這個題目我們直覺得可以使用 Hashtable 的方式來判斷哪些數字出現過，但是這樣題目就太簡單了，所以一般會再有一個額外的限制：空間複雜度為 O(1)。 所以在不使用 Hashtable 的情況下，我們只能用數學的方式去求解，此等差數列正好為梯形公式：(上底 + 下底) * 高 / 2。 接著利用公式的理論總和減去實際總和就是缺少的數字，以上面的例子為例： 123(3 + 9) * 7 / 2 = 423 + 6 + 9 + 7 + 8 + 4 = 3742 - 37 = 5 解法1234567891011121314static int Find(int[] array){ int max = array[0]; int min = array[0]; int sum = 0; for (int i ...

題目在陣列中找出第二大的數字。Find second largest number in an array. 說明找最大的方法我們都會，很簡單地用一個變數去保存目前最大，那找第二大不就可以很簡單的用兩個變數去保存？反之找最小的想法也是一樣，就不在此贅述；這個方法時間複雜度為 O(N)。 解法使用 C# 1234567891011121314151617static int Find(int[] array){ int max = int.MinValue; int second = int.MinValue; for (int i = 0; i < array.Length; ++i) { int n = array[i]; if (n > max) { second = max; max = n; } else if (n > second) second = n; ...

題目計算 1 到 N 總和 (1 + 2 + 3 +…+ N)Sum the Integers from 1 to N. 說明這題看似很簡單，其實真的很簡單，只是可能會有不同要求。一般直覺會使用迴圈解，不過有時候也會要求遞迴解，考你簡單遞迴觀念。 迴圈解1234567int sum(int n){ int sum = 0; for (int i = 1; i <= n; ++i) sum += i; return sum;} 遞迴解123456int sum(int n){ if (n < 1) return 0; return n + sum(n - 1);} 數學解然後不論是迴圈還是遞迴解，都是 O(n) 的時間複雜度，有時候還會要求寫出O(1)的版本，這時候就要拿出數學的思考邏輯了，這沒記錯的話應該是高中數學的範圍。公式如下： 寫成程式 1234int sum(int n){ return n * (n + 1) / 2;} 推導參考維基百 ...

題目從兩個數字中找出最大的一個而不使用判斷描述。There are two int variables: a and b, don’t use “if”, “? :”, “switch” or other judgement statements, find out the biggest one of the two numbers. 說明max(a, b)… 正解，這題題目限制不能用 if、switch 或 ? : 的語法，但沒說不能用 math 的 max。不過這樣就太簡單了，所以我們假定不能用內建函式，而是自己實作這個 max()。 由於不能用判斷式，所以我們依照以下步驟來解： 用利用減法，大減小為正，小減大為負的特性來判斷大小。 至於如何判斷正負，我們看最左邊的 bit 是否為 1，利用上面的 shift 方式得到 sign_bit 為 0 則為正，1 為負。 接著我們利用陣列的索引來代替判斷式，0 為正，表示 a 大，所以 0 的位置放 a；反之 1 為負，b 大，1 的位置放 b。 解法1234567int max(int a, int b){ int ...

題目不使用暫存變數交換兩個變數。Swap two variables without using a temporary variable. 解法常見的方法有以下方式： 加減法123a = a + bb = a - ba = a - b 乘除法123a = a * bb = a / ba = a / b XOR 法123a = a ^ bb = a ^ ba = a ^ b 由於使用加減乘除有可能會有溢位 (overflow) 的問題，所以最好的方式是使用位元運算的 XOR。 說明加減乘除我們用數學角度來看很好理解，以加減為例： 1234假設 X、Y 和 Z 為未知數，a 和 b 為已知數，已知：X = a + bY = X - bZ = X - Y X 代入第二式 1Y = (a + b) - b = a 接著將 X 和 Y 代入 Z，可得 1Z = (a + b) - a = b 回頭和程式對比，可以發現 Y 相當於 b 變數，Z 相當於 a 變數。 使用位元運算並不好去理解為什麼這樣子做就可以達到交換的目的，首先要瞭解以下三點： XOR 定義：有且僅有一個為真，換句 ...

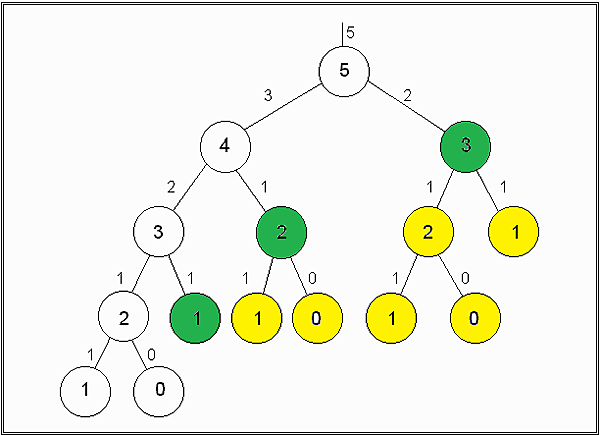
簡介費波那西數列 (Fibonacci)，又稱費氏數列、黃金分割數列等很多譯名，由西方的數學家費波那西使用兔子問題來描述這個數列，以下引用 Wiki： 第一個月初有一對剛誕生的兔子 第二個月之後(第三個月初)牠們可以生育 每月每對可生育的兔子會誕生下一對新兔子 兔子永不死去 使用數學式來表達的話如下： 123F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2) 列出前20個數值 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 F20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 演算法數學法解法有很多種，可以直接套數學公式，推導過程可參考 Wiki，公式如下： 以程式設計的角度來看，一般使用迭代法、Divide and Conquery 和動態規劃 (Dynamic Programming) 的方式來解。 迭代法由於每次新的問題的答案來自於前兩個問題，所以每次運 ...

簡介Dynamic Programming 中文譯作動態規劃，動態規劃類似 Divide and Conquer，一個問題的答案來相依於子問題，常用來解決最佳解的問題。與 Divide and Conquer 不同的地方在於，動態規劃多使用了 memoization 的機制，將處理過的子問題答案記錄下來，避免重複計算，因此在子問題重疊的時候應該使用動態規劃；Divide and Conquer 通常使用遞迴 (Top-Down) 來處理，有時轉成迴圈 (Bottom-up) 來解並不容易，故使用動態規劃則可以解決重覆計算並保留遞迴思考的優點。 同樣拿費波那西數列 (Fibonacci) 為例子 使用 Divide and Conquer 的寫法如下： 12345678function Fibonacci(n) if n == 0 return 0 if n == 1 return 1 end if return Fibonacci(n - 1) + Fibonacci(n - 2)end function 如同之前在 Divide and conquer 一文中所說，會重覆計算黃 ...

說明本文針對一些 JavaScript 效能相關的文章之理論進行實際的測試與驗證，結果有些符合預期，有些則意料之外。測試環境瀏覽器如下： Chrome：18.0.1025.168 m Firefox：12.0 Safari：5.1.5(7534.55.3) Opera：11.62 IE8、IE7 為使用 IE9 切換模式 變數存取JavaScript 變數存取具有以下特性： 使用變數時會透過作用域鏈 (Scope Chain) 自動判斷其所屬範圍，會從目前區域變數查找，逐漸往外圍查找。對變數存取屬性 (點符號.) 會進行查找而消耗時間。 根據以上原則，我們可以推論出一些增加效能的可能方法並實際測試： 使用區域變數，減少變數查找次數，包含作用域鏈與存取屬性，盡可能的使用區域變數。 Chrome Firefox Safari Opera IE9 IE8 IE7 存取區域變數 14.9 15.4 62.8 58.3 30 25 30 存取全域變數 13.8 17 73.9 74.1 43.7 11165.7 11208.6 存取變數屬性 15.3 12.9 80 ...

簡介Iterative Method 中文翻譯作迭代法或疊代法，而在數學領域和電腦程式領域的定義有些不同，數學領域的迭代法指的是無法使用公式一次求解，而須反覆運算求出近似解；而在電腦程式雖然亦有反覆運算的含義，但一般指的是迴圈解。 迭代法透過設定一個初始值開始反覆運算，最後求出答案，是算是一種 Bottom-Up 的模式，通常會和遞迴作比較，實作方式簡易區分如下： 迭代：使用迴圈實作。 遞迴：函式推疊呼叫。 基本上相同的演算法如果能夠直接使用迴圈，因為不透過函式堆疊，效能會比較好。相對於迭代，遞迴就算是一種 Top-Down 的模式。以階乘為範例： 遞迴123456function Factorial(n) if n == 1 return 1 end if return n * Factorial(n - 1)end function 遞迴的思考模式，求 n 階的時候當作 n - 1 階已知，相乘即是答案，n - 1 的如何求在 n 階的時候無須理會，就像上級要交由下屬去處理的 Top-Down 模式。 迭代1234567function Factorial(n) sum = ...