程式技術

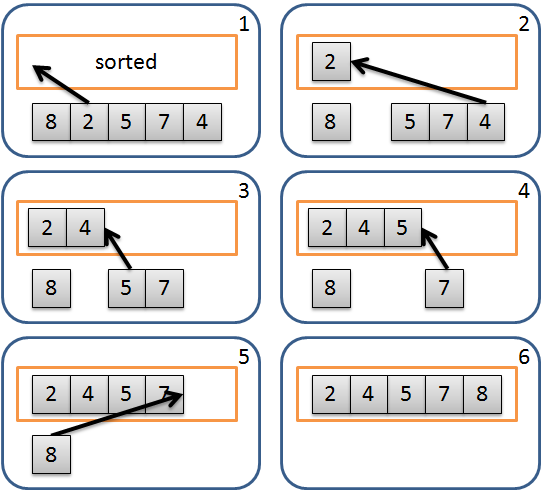
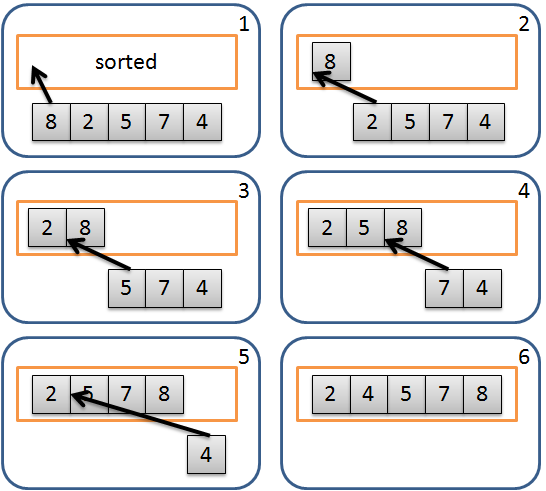
簡介選擇排序法 (Selection Sort) 是排序演算法的一種，也是一種簡單容易理解的演算法，其概念是反覆從未排序的數列中取出最小的元素，加入到另一個的數列，結果即為已排序的數列。運算流程如下： 從未排序的數列中找到最小的元素。 將此元素取出並加入到已排序數列最後。 重複以上動作直到未排序數列全部處理完成。 流程示意圖： 然而實作上通常不使用額外的數列來儲存已排序的部分，而使用原地 (In-place) 的方式來完成，數列的左半部表示已排序部分，右半部表示未排序部分，不另外使用數列。從未排序部分找到最小的元素，利用交換的方式將元素放置已排序部分的尾端。運算流程如下： 從未排序的數列中找到最小的元素。 將此元素與已排序部分的尾端元素進行交換。 重複以上動作直到未排序數列全部處理完成。 流程示意圖： 選擇排序法的比較複雜度固定是 O(n^2)，不過交換次數則是 O(n)，在最佳情況可以到 O(0)，比起氣泡排序法的比較次數少很多，所以效能上會比較好。 分析 最佳時間複雜度：O(n^2) 平均時間複雜度：O(n^2) 最差時間複雜度：O(n^2) 空間複雜度：O(1) Stab ...

資訊 路徑：Tournament \ 1-16 \ 2 - Inv 2001 Semi A+B \ ChessCover 分數：1000 題目說明在西洋棋中要避免你的 King 被攻擊，現在撰寫一套程式，系統輸入棋盤目前狀態，程式要從棋盤上找出安全的位置並回傳有多少個。棋盤上會出現以下五種棋子： Queen：可以攻擊八方位直線。 Rook：可以攻擊上下左右直線。 Bishop：可以攻擊斜角四方位直線。 Knight：可以攻擊 L 位置 (類似象棋馬的日字形)。 Pawn：可以攻擊斜角四方位一格。 如下圖所示： 12345678 Queen Rook Bishop Knight PawnX + + X + + X + + + X + + + X + + + + + X + + + + + + + + + + + + + ++ X + X + X + + + + X + + + + X + + + X + + + X + X + + + + + + + + ++ + X X X + + + ...

簡介插入排序法 (Insertion Sort) 是排序演算法的一種，他是一種簡單容易理解的排序演算法，其概念是利用另一個數列來存放已排序部分，逐一取出未排序數列中元素，從已排序數列由後往前找到適當的位置插入。運算流程如下： 從未排序數列取出一元素。 由後往前和已排序數列元素比較，直到遇到不大於自己的元素並插入此元素之後；若都沒有則插入在最前面。 重複以上動作直到未排序數列全部處理完成。 流程示意圖： 然而實作上通常不使用額外的數列來儲存已排序的部分，而使用原地 (In-place) 的方式來完成，數列的左半部表示已排序部分，右半部表示未排序部分，不另外使用數列。在與已排序的部分比較時，利用指派 (Assign) 的方式將元素往右位移，來達到插入的效果，因為位移的關係需要有另一個變數來暫存最右邊的數值。運算流程如下： 將未排序的部分最左邊元素儲存到暫存變數。 由後往前和已排序部分元素比較，若比自己大則將該元素往右邊位移。 重複2的動作直到遇到不大於自己的元素，將暫存變數寫入在該元素之後；若都沒有則寫入在最前面。 重複以上動作直到未排序部分全部處理完成。 流程示意圖： 分析 最佳 ...

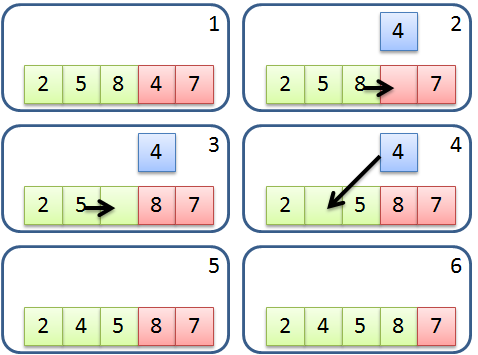
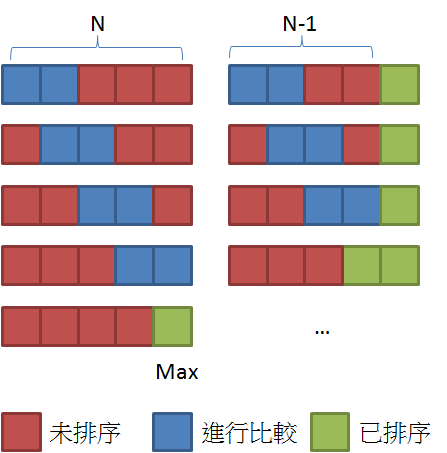
簡介氣泡排序法 (Bubble Sort) 是最容易理解和實作的一種排序演算法，也翻譯作冒泡排序法。由於它很容易學習，所以也是許多演算法課程中第一個學習的排序演算法。 由於他的演算法過程會將最大的數值移動到陣列最後面，而較小的數值則逐漸的往陣列前端移動，就像有許多氣泡慢慢從底部浮出，因此稱為氣泡排序法。他的運作流程如下： 比較相鄰的兩個元素，若前面的元素較大就進行交換。 重複進行 1 的動作直到最後面，最後一個元素將會是最大值。 重複進行 1, 2 的動作，每次比較到上一輪的最後一個元素。 重複進行以上動作直到沒有元素需要比較。 流程示意圖： 實作上直接使用迴圈就可以很容易的完成。另外可以使用額外的旗標 (Flag) 來判斷這一輪是否有發生交換情形，若都沒有發生交換表示數列已經是排序好的，即可跳出迴圈，因此最佳時間複雜度是有可能達到 O(n)。 分析 最佳時間複雜度：O(n) 平均時間複雜度：O(n^2) 最差時間複雜度：O(n^2) 空間複雜度：O(1) Stable sort：是 虛擬碼一般版本1234567891011function sort(list) // 重複 N ...

簡介排序 (Sorting) 演算法是常用到的一種演算法，顧名思義他是用來將資料依據特定的規則做排序後輸出；既然稱為排序就會有一個比較順序的依據，例如數字就比較數值大小、字串則依 ASCII 字母順序或者物件會有自定義的規則。一般沒有特別指定的話，輸出是以遞增排序為準。 穩定排序排序演算法分為穩定 (Stable) 和不穩定 (Unstable) 兩種，是指當資料中有相等數值的兩元素，經過排序之後是否能夠保持原有的相對位置，例如： 1(猴子, 智商60) (丁丁, 智商20) (拉拉, 智商20) (路人甲, 智商90) 將這些資料依據智商來排序，會發現智商 20 的有兩位，因此我們可能得到以下兩種情況 12(丁丁, 智商20) (拉拉, 智商20) (猴子, 智商60) (路人甲, 智商90)(拉拉, 智商20) (丁丁, 智商20) (猴子, 智商60) (路人甲, 智商90) 第一種情況丁丁和拉拉與原始的相對位置一致 (丁丁在前)，能夠總是維持相對位置的排序法我們稱之為穩定排序，反之則稱為不穩定排序，不能確保相對位置與原來一樣 (但是也有可能一樣)。 如果是純數字的排序基本上是 ...

資訊 路徑：Tournament \ 1-16 \ 2 - Inv 2001 Semi A+B \ Tothello 分數：500 題目程式介面12345Class Name: TothelloMethod Name: bestMoveParameters: String[], String[], StringReturns: intMethod signature (be sure your method is public): int bestMove(String[] redPieces, String[] blackPieces, String whoseTurn); 說明Tothello 是一個 Othello 遊戲的修改版，Othello 是一種兩人玩的遊戲，一方使用紅色的棋子，一方使用黑色的棋子，輪流在一個 8x8 大小的棋盤上下棋。當一方下棋之後，如果有將對方的棋子兩端包夾起來，對方的棋子就會變成自己的棋子；而若有棋子變成自己的棋子後，又產生其他的包夾，則又可以變成自己的棋子，直到沒有任何包夾。另外自己的回合的時候，也可以選擇 Pass 不下棋。 現在請實作一個程 ...

簡介連結串列 (Linked List 或稱鏈結串列) 是串列 (List) 的一種，是一種常見的資料結構，利用這個資料結構也能進一步實作出其他的資料結構，例如堆疊 (Stack) 和佇列 (Queue) 等。 它的特性是能夠不使用連續的記憶體空間的情況下，能夠保有並使用一份連續的資料；相對來看，陣列則需要使用連續的記憶體空間。 他的的實作方式是每個節點除了記錄資料之外，還使用額外的指標指向下一個節點，將節點以此方式串連起來形成一個連結串列。 由以上的說明可以知道，使用連結串列的優點如下： 不需使用連續記憶體空間，不需事先指定串列大小。 能夠容易的修改指標，插入或移除節點。 但也有缺點如下： 使用額外的記憶體空間紀錄節點指標。 無法快速索引到某個節點，必須迭代搜索。 此資料結構可以實作的操作變化相當多，這裡實作以下幾種操作： getFirst：取得第一個節點。 getLast：取得最後一個節點。 addFirst：加入節點在最前面。 addLast：加入節點到最後。 addBefore：加入節點在某節點之前。 addAfter：加入節點在某節點之後。 removeFirst： ...

簡介佇列 (Queue) 中文也翻作隊列，顧名思義是一種像排隊一樣的概念，以生活中的情況為例如下圖 人們一個接一個的從隊伍後面加入排隊，而窗口的服務人員則從最前面的民眾一個接一個處理事務；當然現實生活是會有中途離開的人，而在程式世界裡面一般情況是不會有。 在這個模式下我們可以知道他是一種先進先出 (First-In-First-Out, FIFO) 的排程，而在此資料結構中至少會實作兩個操作： enqueue：將資料放入佇列尾端。(註：C++ 中用 push、Java 用 offer、也有 add 等不同的用字) dequeue：取出佇列前端之資料。(註：C++ 中用 pop、Java 用 poll、也有 remove 等不同的用字) 有時候也會多實作一些額外的操作以方便使用，例如： peek：看佇列前端的資料而不取出。(註：也有 front 等不同的用字) size：取得佇列的數目。 在實作上一般使用連結串列 (LinkedList) 來實作，使用陣列同樣可以達成，但較為複雜： 連結串列用指標將資料串起來，將新的東西不斷接在最後面，而取出時則移除最前面的東西即可。由於加入和移 ...

簡介堆疊 (Stack) 是資料結構的一種，是一種很基本常見的資料結構，首先利用現實生活中的例子來說明，如下圖 假設你有一些書把他們疊起來，一層一層的往上疊，所以每次新的書本會放在最上面，而當想要拿取書本的時候，也是從最上面的開始拿。當然現實生活會有可能從中間抽出書本，不過在程式中是不可以的，在程式世界下圖會更貼切。 所以他是一種後進先出 (Last-In-First-Out, LIFO) 的排程，而在此資料結構中至少會實作兩個操作： push：將資料放入堆疊頂端 pop：取出堆疊頂端之資料 有時候也會多實作一些額外的操作以方便使用，例如： peek：看堆疊頂端的資料而不取出。。(註：也有 top 等不同的用字) size：取得堆疊的數目。 在實作上一般可以使用陣列或連結串列 (LinkedList) 兩種方式來實作： 陣列堆疊建立時即建立一個陣列，並使用一個索引來記錄目前所指到的位址，新增或移除資料時，同步修改索引位址；如果有實作堆疊數目的功能時，這數字正好可做為此索引之用。優點是不用處理指標鏈結建立與移除，缺點是容量超過陣列大小時需要額外處理。 連結串列用指標將資料串起來， ...

簡介先來描述一下問題，這裡以下樓梯為例： 有一個人下樓梯，一次可以走一階或兩階，假設總共有N階樓梯，共有幾總走法？例如 N = 3，他可以走 1 + 1 + 1 、1 + 2 或 2 + 1 三種走法。 實做一個程式能夠輸入 N，能回傳共有幾總走法。 演算法這個問題直接使用 Bottom-Up 可能不容易思考，所以我們先利用遞迴的 Top-Down 思考邏輯來想這個問題，結果我們很容易就可以這樣想： 第N階的走法相當於在 N - 1 階的時候走一階過來，或者在 N - 2 階的時候走兩階過來；換句話說，就是第N階的走法等於N - 1階的走法加上N - 2階的走法。 所以我們就可以寫出遞迴式： 123F(N) = F(N - 1) + F(N - 2)F(1) = 1F(2) = 2 列出來的式子和費波那西數列 (Fibonacci) 還蠻像的，我們可以用不同的方式去實做解這問題，這問題較適合用動態規劃 (Dynamic Programming) 去解，直接用 Divide and Conquer 會重覆計算子問題。由於此問題和費波那西數列相當相似，這邊只簡單實做迭代法和動態規 ...