演算法 - 動態規劃 (Dynamic Programming)
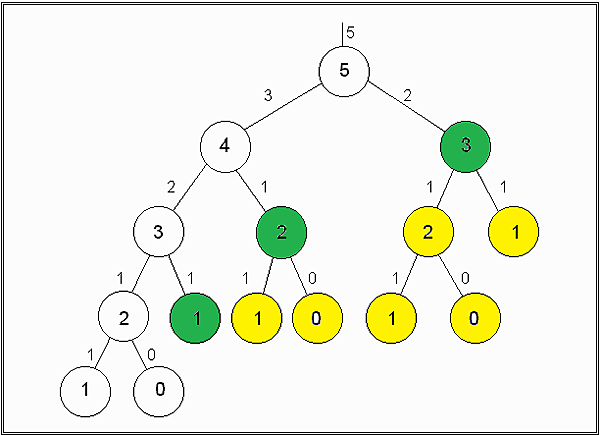
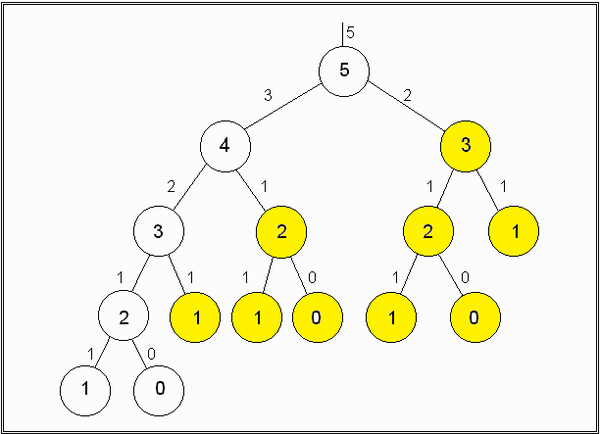
簡介Dynamic Programming 中文譯作動態規劃,動態規劃類似 Divide and Conquer,一個問題的答案來相依於子問題,常用來解決最佳解的問題。與 Divide and Conquer 不同的地方在於,動態規劃多使用了 memoization 的機制,將處理過的子問題答案記錄下來,避免重複計算,因此在子問題重疊的時候應該使用動態規劃;Divide and Conquer 通常使用遞迴 (Top-Down) 來處理,有時轉成迴圈 (Bottom-up) 來解並不容易,故使用動態規劃則可以解決重覆計算並保留遞迴思考的優點。 同樣拿費波那西數列 (Fibonacci) 為例子 使用 Divide and Conquer 的寫法如下: 12345678function Fibonacci(n) if n == 0 return 0 if n == 1 return 1 end if return Fibonacci(n - 1) + Fibonacci(n - 2)end function 如同之前在 Divide and conquer 一文中所說,會重覆計算黃 ...
演算法 - 迭代法 (Iterative)
簡介Iterative Method 中文翻譯作迭代法或疊代法,而在數學領域和電腦程式領域的定義有些不同,數學領域的迭代法指的是無法使用公式一次求解,而須反覆運算求出近似解;而在電腦程式雖然亦有反覆運算的含義,但一般指的是迴圈解。 迭代法透過設定一個初始值開始反覆運算,最後求出答案,是算是一種 Bottom-Up 的模式,通常會和遞迴作比較,實作方式簡易區分如下: 迭代:使用迴圈實作。 遞迴:函式推疊呼叫。 基本上相同的演算法如果能夠直接使用迴圈,因為不透過函式堆疊,效能會比較好。相對於迭代,遞迴就算是一種 Top-Down 的模式。以階乘為範例: 遞迴123456function Factorial(n) if n == 1 return 1 end if return n * Factorial(n - 1)end function 遞迴的思考模式,求 n 階的時候當作 n - 1 階已知,相乘即是答案,n - 1 的如何求在 n 階的時候無須理會,就像上級要交由下屬去處理的 Top-Down 模式。 迭代1234567function Factorial(n) sum = ...
演算法 - 最大子序列 (Maximum Subarray)
簡介最大子序列 (Maximum Subarray 或稱作 Maximum Subsequence) 為在一個具有正負數陣列當中,找出一段連續的元素總和最大,這個問題又分為一定要取值或可不取。實作方法有很多種,這裡說明四種實作方法,分別為暴力法、改良式暴力法、Divide and Conquer 和 Kadane’s 演算法 (Dynamic Programming),其中 Kadane’s 實作取值和可不取值兩種版本,其他為一定要取值版本。 演算法暴力法最簡單直覺的想就是將所有可能的開始和結束範圍都算過一遍即可,[0] ~ [0]、[0] ~ [1] … [0] ~ [N] … [N] ~ [N] 的總和找出最大。 改良式暴力法然而在上面暴力法計算,[0] ~ [N] 的總和時,其實過程中 [0] ~ [0]、[0] ~ [1] … [0] ~ [N] 的總和也已經同時計算了,所以只需計算 [0] ~ [N]、[1] ~ [N] … [N] ~ [N] 即可。 Divide and Conquer如下圖所示,Divide and Conquer 的基本概念是,將數列分成兩塊,各自回報 ...
演算法 - 二元搜索法 (Binary Search)
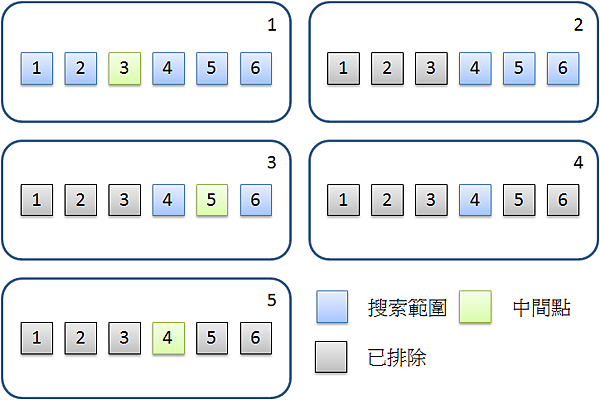
簡介二元搜索法 (Binary Search) 又稱折半搜索,搜索演算法的一種,可使用 Divide and Conquer 或直接使用迴圈 (迭代) 來實作,搜索的目標資料必須是已經排序過的 (以小到大排序為例)。其概念是每次挑選中間位置的資料來比對,若該資料小於目標值,則縮小範圍為左半部,反之亦然;因此使用這個方法每次比對後都可以濾掉一半的資料,以增快搜索速度。過程依以下步驟進行: 取出搜索範圍中點的元素。 與搜索目標比較,若相等則回傳位址。若小於則將左邊邊界改為中點右側,若大於則將右邊邊界改為中點左側。 左邊邊界不超過右邊邊界(還有資料)則重複以上動作,若已無資料則回傳-1(找不到)。 流程範例如圖所示,例如搜索值為4的元素: 分析 最佳時間複雜度:O(1) 平均時間複雜度:O(log n) 最差時間複雜度:O(log n) 空間複雜度:O(1) 虛擬碼迭代12345678910111213141516function search(list, target) var left = 0, right = list.length - 1 while left <= ri ...
演算法 - 快速排序法 (Quick Sort)
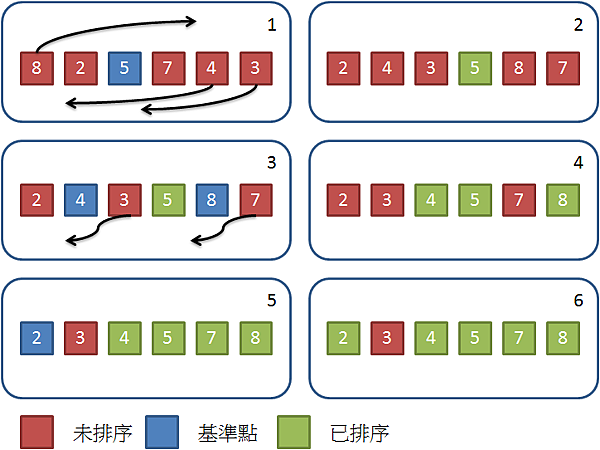
簡介快速排序法是排序演算法的一種,使用 Divide and Conquer 的演算法來實作。其概念是從數列中挑選一個基準點,大於基準的放一邊,小於的放一邊,如此循環最後可完成排序。過程依照以下步驟進行(遞增為例): 數列中選擇一元素作為基準點 (pivot)。 小於此元素的移至基準的左邊,大於此元素的移至右邊,相等的任意放。 基準點左邊和右邊視為兩個數列,並重複做以上動作直到數列剩下一個或零個元素。 流程範例如圖所示: 實作的方式除了一般使用額外的暫存數列之外,也有使用較少額外空間的 原地 (In-place) 方式,In-place 的方式主要概念是將基準點暫時移到最右邊,小於基準的移至數列一端並記錄遞增索引,最後將基準點換回索引位置,過程依照以下步驟進行 (遞增為例): 數列中選擇一元素作為基準點 (pivot),並與最右邊的元素交換位置。 建立一索引指向最左邊元素。 小於基準的元素與索引位置的元素交換位置,每次交換後遞增索引。 完成後將基準點與索引位置的元素交換位置。 基準點左邊和右邊視為兩個數列,並重複做以上動作直到數列剩下一個或零個元素。 流程範例如圖所示: 基準點 ...
演算法 - 合併排序法 (Merge Sort)
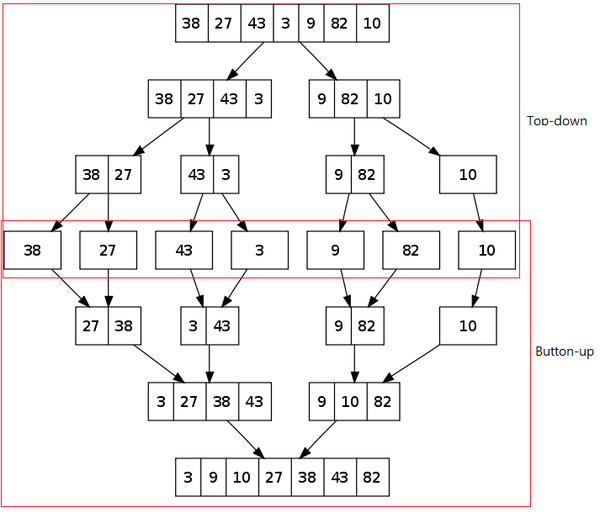
簡介合併排序法 (或稱歸併排序法),是排序演算法的一種,使用 Divide and Conquer 的演算法來實作。排序時需要額外的空間來處理,過程依照以下步驟進行: 將陣列分割直到只有一個元素。 開始兩兩合併,每次合併同時進行排序,合併出排序過的陣列。 重複2的動作直到全部合併完成。 流程範例如圖所示: 實作又可分為 Top-down 和 Bottom-up,依據原始的步驟會先將陣量分割直到剩一個元素 (Top-down),然而也可以一開始就直接切割成單一元素開始合併 (Bottom-up)。 分析 最佳時間複雜度:O(nlog n) 平均時間複雜度:O(nlog n) 最差時間複雜度:O(nlog n) 空間複雜度:O(n) Stable sort:是 虛擬碼以下以較高階的想法寫出虛擬碼,實作上效能要好必須還要進一步修改: Top-down12345678910111213141516171819202122function sort(list) if list.length == 1 return list end if left = 取出從 list[0] 到 list ...
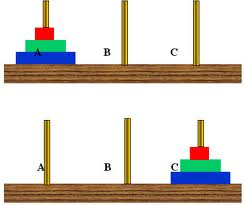
演算法 - 河內塔 (Tower of Hanoi)
簡介也翻譯作漢諾塔,這是根據一個傳說演變而成的題目,題目的規則如下: 有三根竿子,例如編號為 A、B 和 C,竿子上面可串中空圓盤。 於 A 竿子放入 N 個盤子開始,盤子由下至上變小。 一次只能移動一個盤子。 大盤子不能再小盤子上面。 目標將全部盤子移動到 C 竿子。 現在我們嘗試上面的問題撰寫成程式解決,依據上面的說明,寫出程式印出移動的步驟。 演算法此題目一般可使用 Divide and Conquer 來解,當有 N 個盤子的時候很難思考,我們假設只有兩個盤子的時候,就很好思考,只需要: 將上面的盤子移到暫時擺放的竿子。 將下面的盤子移到目標竿子。 將原來上面的盤子移到目標竿子。 而當盤子 N 個的時候,其實也是依照同樣的邏輯進行即可,但上面 N - 1 個盤子要如何移到暫時擺放的竿子,這時候我們用遞迴的方式交給下一次呼叫自己去處理。 虛擬碼123456789function move(disks, from, to) if disks == 1 自訂的移動動作 else move(disks - 1, from, 另一竿子) move(1, from, ...
演算法 - 分治法 (Divide and conquer)
簡介Divide and conquer 中文翻作分治法,概念如字面上的意義,將問題先切分成小問題後再解決,再將結果合併求出原始問題的答案。 優點Divide and conquer 有許多優點,舉出常見的幾點如下: 將困難的問題簡化為容易實作的方式,例如河內塔 (Tower of Hanoii) 問題。 提升程式效率,例如合併排序 (Merge Sort) 讓排序速度提升。 能夠平行處理,例如 MapReduce 也是 Divide and conquer 的一種。 步驟以下摘錄自 Wiki 分解:將原問題分解為若干個規模較小,相對獨立,與原問題形式相同的子問題。 解決:若子問題規模較小且易於解決時,則直接解。否則,遞歸地解決各子問題。 合併:將各子問題的解合併為原問題的解。 不適合的情況Divide and conquer 是利用遞迴的方式來實作,所以當不適合使用遞迴的時候也就不適合使用 Divide and conquer,例如費波那西數列 (fibonacci): 雖然費波那西數列使用 Divide and conquer 來思考很容易實作,但可以從圖中看到,單純使用遞 ...