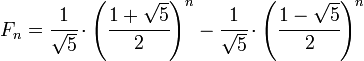演算法

題目在陣列中找出第 K 大的數字。Find Kth largest number in an array. 說明找第 K 大的數字，我們可以直覺的用排序後就可以找出來，時間複雜度取決於排序演算法，例如使用快速排序法為 O(n log n)。 另外一個方法是延續前一個題目的想法，找第 K 大就用 K 個變數去保存？不過由於 K 也是個變數，所以我們需利用動態的資料結構來保存，這個 Case 使用 Linked List 是最合適。時間複雜度則為 O(n K)，而當 K 很小的時候可以接近 O(n)的效能，反之，K 很大的時候，可能會比直接用快速排序法還慢。 解法123456789101112131415static int Find(int[] array, int k){ List list = new List(); for (int i = 0; i < array.Length; ++i) { int n = array[i]; int j = 0; for (int length = Math ...

題目計算 1 * 2 + 2 * 3 +…+ (n-1) * n 總和。Write a function to calculate 1 * 2 + 2 * 3 + … + (N - 1) * N. 說明題目為計算 1 * 2 + 2 * 3 +…+ (n-1) * n 的總和，一樣是求合的問題，同樣使用迴圈或遞迴即可，如果能用數學證明出公式的話，也可以直接套公式。 迴圈解1234567int sum(int n){ int sum = 0; for (int i = 2; i <= n; ++i) sum += (i - 1) * i; return sum;} 遞迴解123456int sum(int n){ if (n < 2) return 0; return (n - 1) * n + sum(n - 1);} 數學解網路上沒有找到比較好的推導，主要概念是將數列拆解為下面兩個數列 然後這兩個數列可以找到公式 最後將兩個式子相減 寫成程式碼 1234int sum ...

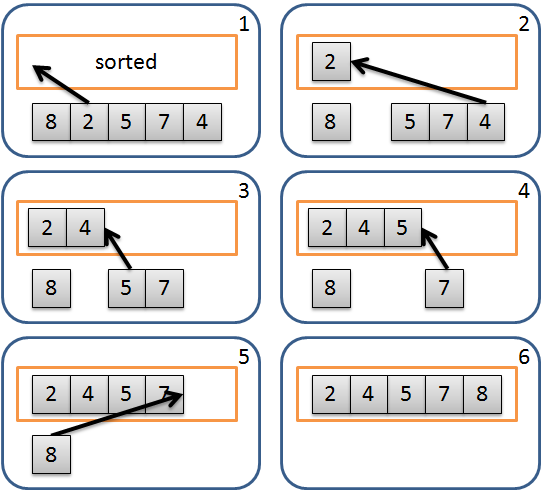
簡介選擇排序法 (Selection Sort) 是排序演算法的一種，也是一種簡單容易理解的演算法，其概念是反覆從未排序的數列中取出最小的元素，加入到另一個的數列，結果即為已排序的數列。運算流程如下： 從未排序的數列中找到最小的元素。 將此元素取出並加入到已排序數列最後。 重複以上動作直到未排序數列全部處理完成。 流程示意圖： 然而實作上通常不使用額外的數列來儲存已排序的部分，而使用原地 (In-place) 的方式來完成，數列的左半部表示已排序部分，右半部表示未排序部分，不另外使用數列。從未排序部分找到最小的元素，利用交換的方式將元素放置已排序部分的尾端。運算流程如下： 從未排序的數列中找到最小的元素。 將此元素與已排序部分的尾端元素進行交換。 重複以上動作直到未排序數列全部處理完成。 流程示意圖： 選擇排序法的比較複雜度固定是 O(n^2)，不過交換次數則是 O(n)，在最佳情況可以到 O(0)，比起氣泡排序法的比較次數少很多，所以效能上會比較好。 分析 最佳時間複雜度：O(n^2) 平均時間複雜度：O(n^2) 最差時間複雜度：O(n^2) 空間複雜度：O(1) Stab ...

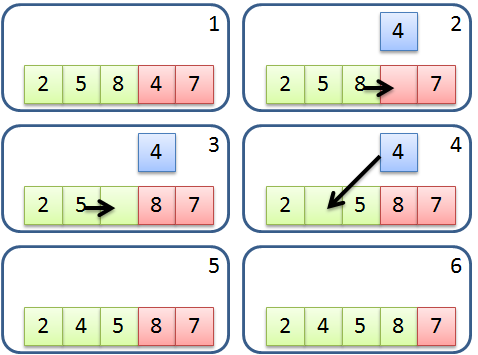
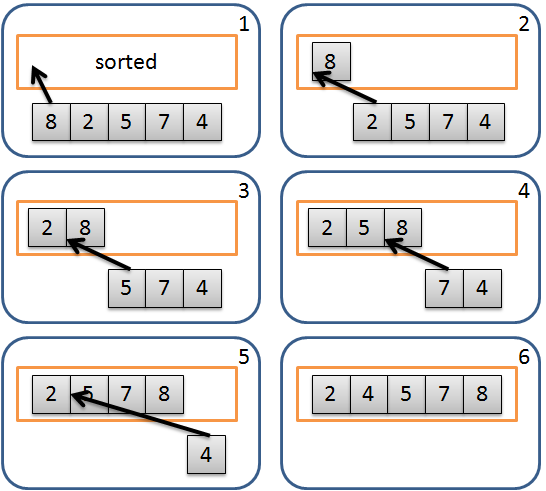
簡介插入排序法 (Insertion Sort) 是排序演算法的一種，他是一種簡單容易理解的排序演算法，其概念是利用另一個數列來存放已排序部分，逐一取出未排序數列中元素，從已排序數列由後往前找到適當的位置插入。運算流程如下： 從未排序數列取出一元素。 由後往前和已排序數列元素比較，直到遇到不大於自己的元素並插入此元素之後；若都沒有則插入在最前面。 重複以上動作直到未排序數列全部處理完成。 流程示意圖： 然而實作上通常不使用額外的數列來儲存已排序的部分，而使用原地 (In-place) 的方式來完成，數列的左半部表示已排序部分，右半部表示未排序部分，不另外使用數列。在與已排序的部分比較時，利用指派 (Assign) 的方式將元素往右位移，來達到插入的效果，因為位移的關係需要有另一個變數來暫存最右邊的數值。運算流程如下： 將未排序的部分最左邊元素儲存到暫存變數。 由後往前和已排序部分元素比較，若比自己大則將該元素往右邊位移。 重複2的動作直到遇到不大於自己的元素，將暫存變數寫入在該元素之後；若都沒有則寫入在最前面。 重複以上動作直到未排序部分全部處理完成。 流程示意圖： 分析 最佳 ...

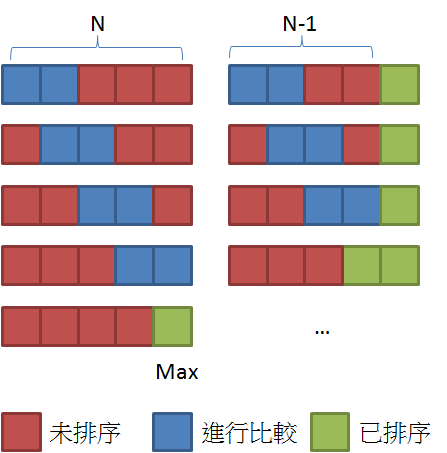
簡介氣泡排序法 (Bubble Sort) 是最容易理解和實作的一種排序演算法，也翻譯作冒泡排序法。由於它很容易學習，所以也是許多演算法課程中第一個學習的排序演算法。 由於他的演算法過程會將最大的數值移動到陣列最後面，而較小的數值則逐漸的往陣列前端移動，就像有許多氣泡慢慢從底部浮出，因此稱為氣泡排序法。他的運作流程如下： 比較相鄰的兩個元素，若前面的元素較大就進行交換。 重複進行 1 的動作直到最後面，最後一個元素將會是最大值。 重複進行 1, 2 的動作，每次比較到上一輪的最後一個元素。 重複進行以上動作直到沒有元素需要比較。 流程示意圖： 實作上直接使用迴圈就可以很容易的完成。另外可以使用額外的旗標 (Flag) 來判斷這一輪是否有發生交換情形，若都沒有發生交換表示數列已經是排序好的，即可跳出迴圈，因此最佳時間複雜度是有可能達到 O(n)。 分析 最佳時間複雜度：O(n) 平均時間複雜度：O(n^2) 最差時間複雜度：O(n^2) 空間複雜度：O(1) Stable sort：是 虛擬碼一般版本1234567891011function sort(list) // 重複 N ...

簡介排序 (Sorting) 演算法是常用到的一種演算法，顧名思義他是用來將資料依據特定的規則做排序後輸出；既然稱為排序就會有一個比較順序的依據，例如數字就比較數值大小、字串則依 ASCII 字母順序或者物件會有自定義的規則。一般沒有特別指定的話，輸出是以遞增排序為準。 穩定排序排序演算法分為穩定 (Stable) 和不穩定 (Unstable) 兩種，是指當資料中有相等數值的兩元素，經過排序之後是否能夠保持原有的相對位置，例如： 1(猴子, 智商60) (丁丁, 智商20) (拉拉, 智商20) (路人甲, 智商90) 將這些資料依據智商來排序，會發現智商 20 的有兩位，因此我們可能得到以下兩種情況 12(丁丁, 智商20) (拉拉, 智商20) (猴子, 智商60) (路人甲, 智商90)(拉拉, 智商20) (丁丁, 智商20) (猴子, 智商60) (路人甲, 智商90) 第一種情況丁丁和拉拉與原始的相對位置一致 (丁丁在前)，能夠總是維持相對位置的排序法我們稱之為穩定排序，反之則稱為不穩定排序，不能確保相對位置與原來一樣 (但是也有可能一樣)。 如果是純數字的排序基本上是 ...

簡介先來描述一下問題，這裡以下樓梯為例： 有一個人下樓梯，一次可以走一階或兩階，假設總共有N階樓梯，共有幾總走法？例如 N = 3，他可以走 1 + 1 + 1 、1 + 2 或 2 + 1 三種走法。 實做一個程式能夠輸入 N，能回傳共有幾總走法。 演算法這個問題直接使用 Bottom-Up 可能不容易思考，所以我們先利用遞迴的 Top-Down 思考邏輯來想這個問題，結果我們很容易就可以這樣想： 第N階的走法相當於在 N - 1 階的時候走一階過來，或者在 N - 2 階的時候走兩階過來；換句話說，就是第N階的走法等於N - 1階的走法加上N - 2階的走法。 所以我們就可以寫出遞迴式： 123F(N) = F(N - 1) + F(N - 2)F(1) = 1F(2) = 2 列出來的式子和費波那西數列 (Fibonacci) 還蠻像的，我們可以用不同的方式去實做解這問題，這問題較適合用動態規劃 (Dynamic Programming) 去解，直接用 Divide and Conquer 會重覆計算子問題。由於此問題和費波那西數列相當相似，這邊只簡單實做迭代法和動態規 ...

題目在陣列中找出第二大的數字。Find second largest number in an array. 說明找最大的方法我們都會，很簡單地用一個變數去保存目前最大，那找第二大不就可以很簡單的用兩個變數去保存？反之找最小的想法也是一樣，就不在此贅述；這個方法時間複雜度為 O(N)。 解法使用 C# 1234567891011121314151617static int Find(int[] array){ int max = int.MinValue; int second = int.MinValue; for (int i = 0; i < array.Length; ++i) { int n = array[i]; if (n > max) { second = max; max = n; } else if (n > second) second = n; ...

題目計算 1 到 N 總和 (1 + 2 + 3 +…+ N)Sum the Integers from 1 to N. 說明這題看似很簡單，其實真的很簡單，只是可能會有不同要求。一般直覺會使用迴圈解，不過有時候也會要求遞迴解，考你簡單遞迴觀念。 迴圈解1234567int sum(int n){ int sum = 0; for (int i = 1; i <= n; ++i) sum += i; return sum;} 遞迴解123456int sum(int n){ if (n < 1) return 0; return n + sum(n - 1);} 數學解然後不論是迴圈還是遞迴解，都是 O(n) 的時間複雜度，有時候還會要求寫出O(1)的版本，這時候就要拿出數學的思考邏輯了，這沒記錯的話應該是高中數學的範圍。公式如下： 寫成程式 1234int sum(int n){ return n * (n + 1) / 2;} 推導參考維基百 ...

簡介費波那西數列 (Fibonacci)，又稱費氏數列、黃金分割數列等很多譯名，由西方的數學家費波那西使用兔子問題來描述這個數列，以下引用 Wiki： 第一個月初有一對剛誕生的兔子 第二個月之後(第三個月初)牠們可以生育 每月每對可生育的兔子會誕生下一對新兔子 兔子永不死去 使用數學式來表達的話如下： 123F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2) 列出前20個數值 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 F20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 演算法數學法解法有很多種，可以直接套數學公式，推導過程可參考 Wiki，公式如下： 以程式設計的角度來看，一般使用迭代法、Divide and Conquery 和動態規劃 (Dynamic Programming) 的方式來解。 迭代法由於每次新的問題的答案來自於前兩個問題，所以每次運 ...