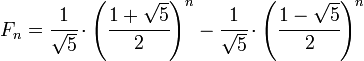上下樓梯問題 & (籃球) 得分問題
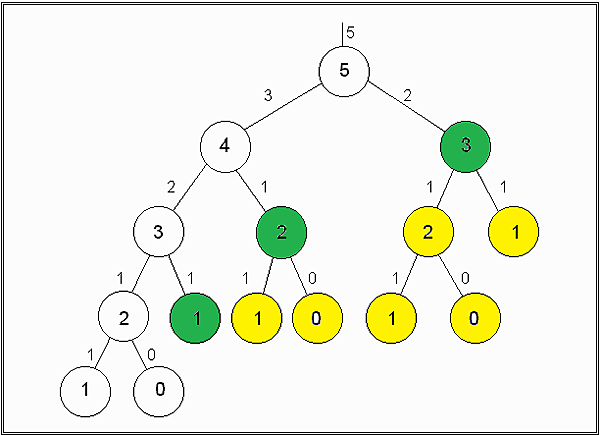
簡介先來描述一下問題,這裡以下樓梯為例: 有一個人下樓梯,一次可以走一階或兩階,假設總共有N階樓梯,共有幾總走法?例如 N = 3,他可以走 1 + 1 + 1 、1 + 2 或 2 + 1 三種走法。 實做一個程式能夠輸入 N,能回傳共有幾總走法。 演算法這個問題直接使用 Bottom-Up 可能不容易思考,所以我們先利用遞迴的 Top-Down 思考邏輯來想這個問題,結果我們很容易就可以這樣想: 第N階的走法相當於在 N - 1 階的時候走一階過來,或者在 N - 2 階的時候走兩階過來;換句話說,就是第N階的走法等於N - 1階的走法加上N - 2階的走法。 所以我們就可以寫出遞迴式: 123F(N) = F(N - 1) + F(N - 2)F(1) = 1F(2) = 2 列出來的式子和費波那西數列 (Fibonacci) 還蠻像的,我們可以用不同的方式去實做解這問題,這問題較適合用動態規劃 (Dynamic Programming) 去解,直接用 Divide and Conquer 會重覆計算子問題。由於此問題和費波那西數列相當相似,這邊只簡單實做迭代法和動態規 ...
演算法 - 費波那西數列 (Fibonacci)
簡介費波那西數列 (Fibonacci),又稱費氏數列、黃金分割數列等很多譯名,由西方的數學家費波那西使用兔子問題來描述這個數列,以下引用 Wiki: 第一個月初有一對剛誕生的兔子 第二個月之後(第三個月初)牠們可以生育 每月每對可生育的兔子會誕生下一對新兔子 兔子永不死去 使用數學式來表達的話如下: 123F(0) = 0F(1) = 1F(n) = F(n-1) + F(n-2) 列出前20個數值 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 F20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 演算法數學法解法有很多種,可以直接套數學公式,推導過程可參考 Wiki,公式如下: 以程式設計的角度來看,一般使用迭代法、Divide and Conquery 和動態規劃 (Dynamic Programming) 的方式來解。 迭代法由於每次新的問題的答案來自於前兩個問題,所以每次運 ...
演算法 - 動態規劃 (Dynamic Programming)
簡介Dynamic Programming 中文譯作動態規劃,動態規劃類似 Divide and Conquer,一個問題的答案來相依於子問題,常用來解決最佳解的問題。與 Divide and Conquer 不同的地方在於,動態規劃多使用了 memoization 的機制,將處理過的子問題答案記錄下來,避免重複計算,因此在子問題重疊的時候應該使用動態規劃;Divide and Conquer 通常使用遞迴 (Top-Down) 來處理,有時轉成迴圈 (Bottom-up) 來解並不容易,故使用動態規劃則可以解決重覆計算並保留遞迴思考的優點。 同樣拿費波那西數列 (Fibonacci) 為例子 使用 Divide and Conquer 的寫法如下: 12345678function Fibonacci(n) if n == 0 return 0 if n == 1 return 1 end if return Fibonacci(n - 1) + Fibonacci(n - 2)end function 如同之前在 Divide and conquer 一文中所說,會重覆計算黃 ...
演算法 - 最大子序列 (Maximum Subarray)
簡介最大子序列 (Maximum Subarray 或稱作 Maximum Subsequence) 為在一個具有正負數陣列當中,找出一段連續的元素總和最大,這個問題又分為一定要取值或可不取。實作方法有很多種,這裡說明四種實作方法,分別為暴力法、改良式暴力法、Divide and Conquer 和 Kadane’s 演算法 (Dynamic Programming),其中 Kadane’s 實作取值和可不取值兩種版本,其他為一定要取值版本。 演算法暴力法最簡單直覺的想就是將所有可能的開始和結束範圍都算過一遍即可,[0] ~ [0]、[0] ~ [1] … [0] ~ [N] … [N] ~ [N] 的總和找出最大。 改良式暴力法然而在上面暴力法計算,[0] ~ [N] 的總和時,其實過程中 [0] ~ [0]、[0] ~ [1] … [0] ~ [N] 的總和也已經同時計算了,所以只需計算 [0] ~ [N]、[1] ~ [N] … [N] ~ [N] 即可。 Divide and Conquer如下圖所示,Divide and Conquer 的基本概念是,將數列分成兩塊,各自回報 ...