簡介
透過一些演算法能夠對樹狀結構的節點進行逐一的訪問,可以應用在搜索、序列化或其他的用途上。依據走訪的方式,大致上可分為以下兩大類:
深度優先 (Depth-first)
深度優先又分為三種走訪方式,而一般樹和二元樹以下分開來討論:
一般樹

前序 (Pre-order)
- 訪問根節點
- 訪問所有子樹
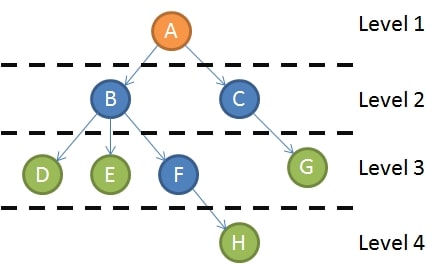
上圖的走訪順序為:ABDEFHCG
中序 (In-order)
- 訪問第一個子樹
- 訪問根節點
- 訪問其他子樹
上圖的走訪順序為:DBEHFAGC
事實上一般樹的情況下,中序走訪並不實用。
後序 (Post-order)
- 訪問所有子樹
- 訪問根節點
上圖的走訪順序為:DEHFBGCA
二元樹

前序 (Pre-order)
- 訪問根節點
- 訪問左子樹
- 訪問右子樹
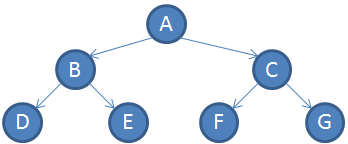
上圖的走訪順序為:ABDECFG
中序 (In-order)
- 訪問左子樹
- 訪問根節點
- 訪問右子樹
上圖的走訪順序為:DBEAFCG
後序 (Post-order)
- 訪問左子樹
- 訪問右子樹
- 訪問根節點
上圖的走訪順序為:DEBFGCA
廣度優先 (Breadth-first)
廣度優先又可以稱為 Level-order,將每一個階層的節點都走訪完後才到下一層。
圖一的走訪順序為:ABCDEFGH
圖二的走訪順序為:ABCDEFG
語法
C#
一般樹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using Tree;
namespace TreeTraversal
{
public class TreeTraversal
{
public static List<T> PreOrder<T>(Tree<T> tree)
{
List<T> list = new List<T>(tree.Count);
PreOrder(tree, list);
return list;
}
private static void PreOrder<T>(Tree<T> tree, List<T> list)
{
list.Add(tree.Value);
foreach (Tree<T> child in tree.Children)
PreOrder(child, list);
}
public static List<T> InOrder<T>(Tree<T> tree)
{
List<T> list = new List<T>(tree.Count);
InOrder(tree, list);
return list;
}
private static void InOrder<T>(Tree<T> tree, List<T> list)
{
IEnumerator<Tree<T>> enu =tree.Children.GetEnumerator();
if (enu.MoveNext())
InOrder(enu.Current, list);
list.Add(tree.Value);
while(enu.MoveNext())
InOrder(enu.Current, list);
}
public static List<T> PostOrder<T>(Tree<T> tree)
{
List<T> list = new List<T>(tree.Count);
PostOrder(tree, list);
return list;
}
private static void PostOrder<T>(Tree<T> tree, List<T> list)
{
foreach (Tree<T> child in tree.Children)
PostOrder(child, list);
list.Add(tree.Value);
}
public static List<T> BreadthFirst<T>(Tree<T> tree)
{
List<T> list = new List<T>(tree.Count);
Queue<Tree<T>> queue = new Queue<Tree<T>>();
queue.Enqueue(tree);
while (queue.Count > 0)
{
Tree<T> tmpTree = queue.Dequeue();
list.Add(tmpTree.Value);
foreach (Tree<T> child in tmpTree.Children)
queue.Enqueue(child);
}
return list;
}
}
}
|
二元樹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using BinaryTree;
namespace TreeTraversal
{
public class BinaryTreeTraversal
{
public static List<T> PreOrder<T>(BinaryTree<T> tree)
{
List<T> list = new List<T>(tree.Count);
PreOrder(tree, list);
return list;
}
private static void PreOrder<T>(BinaryTree<T> tree, List<T> list)
{
list.Add(tree.Value);
if(tree.Left != null)
PreOrder(tree.Left, list);
if (tree.Right != null)
PreOrder(tree.Right, list);
}
public static List<T> InOrder<T>(BinaryTree<T> tree)
{
List<T> list = new List<T>(tree.Count);
InOrder(tree, list);
return list;
}
private static void InOrder<T>(BinaryTree<T> tree, List<T> list)
{
if (tree.Left != null)
InOrder(tree.Left, list);
list.Add(tree.Value);
if (tree.Right != null)
InOrder(tree.Right, list);
}
public static List<T> PostOrder<T>(BinaryTree<T> tree)
{
List<T> list = new List<T>(tree.Count);
PostOrder(tree, list);
return list;
}
private static void PostOrder<T>(BinaryTree<T> tree, List<T> list)
{
if (tree.Left != null)
PostOrder(tree.Left, list);
if (tree.Right != null)
PostOrder(tree.Right, list);
list.Add(tree.Value);
}
public static List<T> BreadthFirst<T>(BinaryTree<T> tree)
{
List<T> list = new List<T>(tree.Count);
Queue<BinaryTree<T>> queue = new Queue<BinaryTree<T>>();
queue.Enqueue(tree);
while (queue.Count > 0)
{
BinaryTree<T> tmpTree = queue.Dequeue();
list.Add(tmpTree.Value);
if (tmpTree.Left != null)
queue.Enqueue(tmpTree.Left);
if (tmpTree.Right != null)
queue.Enqueue(tmpTree.Right);
}
return list;
}
}
}
|
Java
一般樹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| import java.util.ArrayList;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class TreeTraversal {
public static <T> List<T> preOrder(Tree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
preOrder(tree, list);
return list;
}
private static <T> void preOrder(Tree<T> tree, List<T> list)
{
list.add(tree.getValue());
for (Tree<T> child : tree.children())
preOrder(child, list);
}
public static <T> List<T> inOrder(Tree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
inOrder(tree, list);
return list;
}
private static <T> void inOrder(Tree<T> tree, List<T> list)
{
Iterator<Tree<T>> iterator =tree.children().iterator();
if (iterator.hasNext())
inOrder(iterator.next(), list);
list.add(tree.getValue());
while(iterator.hasNext())
inOrder(iterator.next(), list);
}
public static <T> List<T> postOrder(Tree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
postOrder(tree, list);
return list;
}
private static <T> void postOrder(Tree<T> tree, List<T> list)
{
for (Tree<T> child : tree.children())
postOrder(child, list);
list.add(tree.getValue());
}
public static <T> List<T> breadthFirst(Tree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
Queue<Tree<T>> queue = new LinkedList<Tree<T>>();
queue.add(tree);
while (!queue.isEmpty())
{
Tree<T> tmpTree = queue.poll();
list.add(tmpTree.getValue());
for (Tree<T> child : tmpTree.children())
queue.add(child);
}
return list;
}
}
|
二元樹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class BinaryTreeTraversal {
public static <T> List<T> preOrder(BinaryTree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
preOrder(tree, list);
return list;
}
private static <T> void preOrder(BinaryTree<T> tree, List<T> list)
{
list.add(tree.getValue());
if(tree.left() != null)
preOrder(tree.left(), list);
if (tree.right() != null)
preOrder(tree.right(), list);
}
public static <T> List<T> inOrder(BinaryTree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
inOrder(tree, list);
return list;
}
private static <T> void inOrder(BinaryTree<T> tree, List<T> list)
{
if(tree.left() != null)
inOrder(tree.left(), list);
list.add(tree.getValue());
if (tree.right() != null)
inOrder(tree.right(), list);
}
public static <T> List<T> postOrder(BinaryTree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
postOrder(tree, list);
return list;
}
private static <T> void postOrder(BinaryTree<T> tree, List<T> list)
{
if(tree.left() != null)
postOrder(tree.left(), list);
if (tree.right() != null)
postOrder(tree.right(), list);
list.add(tree.getValue());
}
public static <T> List<T> breadthFirst(BinaryTree<T> tree)
{
List<T> list = new ArrayList<T>(tree.size());
Queue<BinaryTree<T>> queue = new LinkedList<BinaryTree<T>>();
queue.add(tree);
while (!queue.isEmpty())
{
BinaryTree<T> tmpTree = queue.poll();
list.add(tmpTree.getValue());
if (tmpTree.left() != null)
queue.add(tmpTree.left());
if (tmpTree.right() != null)
queue.add(tmpTree.right());
}
return list;
}
}
|
C++
一般樹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| #ifndef TREETRAVERSAL_H
#define TREETRAVERSAL_H
#include <vector>
#include <queue>
#include "Tree.h"
using namespace std;
template<typename T>
class TreeTraversal
{
public:
TreeTraversal() {}
virtual ~TreeTraversal() {}
static vector<T>& preOrder(Tree<T>* tree)
{
vector<T>* vect = new vector<T>();
preOrder(tree, *vect);
return *vect;
}
static vector<T>& inOrder(Tree<T>* tree)
{
vector<T>* vect = new vector<T>();
inOrder(tree, *vect);
return *vect;
}
static vector<T>& postOrder(Tree<T>* tree)
{
vector<T>* vect = new vector<T>();
postOrder(tree, *vect);
return *vect;
}
static vector<T>& breadthFirst(Tree<T>* tree)
{
vector<T>* vect = new vector<T>();
queue<Tree<T>*> queue;
queue.push(tree);
while (!queue.empty())
{
Tree<T>* tmpTree = queue.front();
queue.pop();
vect->push_back(tmpTree->getValue());
TreeList<string>* children = tmpTree->children();
children->begin();
while(Tree<string>* child = children->next())
queue.push(child);
}
return *vect;
}
protected:
private:
static void preOrder(Tree<T>* tree, vector<T>& vect)
{
vect.push_back(tree->getValue());
TreeList<string>* children = tree->children();
children->begin();
while(Tree<string>* child = children->next())
preOrder(child, vect);
}
static void inOrder(Tree<T>* tree, vector<T>& vect)
{
TreeList<string>* children = tree->children();
children->begin();
if(Tree<string>* child = children->next())
inOrder(child, vect);
vect.push_back(tree->getValue());
while(Tree<string>* child = children->next())
inOrder(child, vect);
}
static void postOrder(Tree<T>* tree, vector<T>& vect)
{
TreeList<string>* children = tree->children();
children->begin();
while(Tree<string>* child = children->next())
postOrder(child, vect);
vect.push_back(tree->getValue());
}
};
#endif
|
二元樹
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
| #ifndef BINARYTREETRAVERSAL_H
#define BINARYTREETRAVERSAL_H
#include <vector>
#include <queue>
#include "BinaryTree.h"
using namespace std;
template<typename T>
class BinaryTreeTraversal
{
public:
BinaryTreeTraversal() {}
virtual ~BinaryTreeTraversal() {}
static vector<T>& preOrder(BinaryTree<T>* tree)
{
vector<T>* vect = new vector<T>();
preOrder(tree, *vect);
return *vect;
}
static vector<T>& inOrder(BinaryTree<T>* tree)
{
vector<T>* vect = new vector<T>();
inOrder(tree, *vect);
return *vect;
}
static vector<T>& postOrder(BinaryTree<T>* tree)
{
vector<T>* vect = new vector<T>();
postOrder(tree, *vect);
return *vect;
}
static vector<T>& breadthFirst(BinaryTree<T>* tree)
{
vector<T>* vect = new vector<T>();
queue<BinaryTree<T>*> queue;
queue.push(tree);
while (!queue.empty())
{
BinaryTree<T>* tmpTree = queue.front();
queue.pop();
vect->push_back(tmpTree->getValue());
if (tmpTree->left() != 0)
queue.push(tmpTree->left());
if (tmpTree->right() != 0)
queue.push(tmpTree->right());
}
return *vect;
}
protected:
private:
static void preOrder(BinaryTree<T>* tree, vector<T>& vect)
{
vect.push_back(tree->getValue());
if(tree->left() != 0)
preOrder(tree->left(), vect);
if (tree->right() != 0)
preOrder(tree->right(), vect);
}
static void inOrder(BinaryTree<T>* tree, vector<T>& vect)
{
if(tree->left() != 0)
inOrder(tree->left(), vect);
vect.push_back(tree->getValue());
if (tree->right() != 0)
inOrder(tree->right(), vect);
}
static void postOrder(BinaryTree<T>* tree, vector<T>& vect)
{
if(tree->left() != 0)
postOrder(tree->left(), vect);
if (tree->right() != 0)
postOrder(tree->right(), vect);
vect.push_back(tree->getValue());
}
};
#endif
|
延伸閱讀
樹 (Tree)
二元樹 (Binary Tree)
二元搜索樹 (Binary Search Tree)
一般樹轉二元樹