演算法

簡介

也翻譯作漢諾塔，這是根據一個傳說演變而成的題目，題目的規則如下：

有三根竿子，例如編號為 A、B 和 C，竿子上面可串中空圓盤。
於 A 竿子放入 N 個盤子開始，盤子由下至上變小。
一次只能移動一個盤子。
大盤子不能再小盤子上面。
目標將全部盤子移動到 C 竿子。

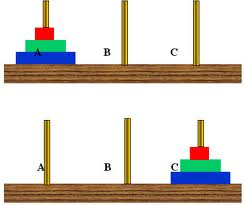
現在我們嘗試上面的問題撰寫成程式解決，依據上面的說明，寫出程式印出移動的步驟。

此題目一般可使用 Divide and Conquer 來解，當有 N 個盤子的時候很難思考，我們假設只有兩個盤子的時候，就很好思考，只需要：

將上面的盤子移到暫時擺放的竿子。
將下面的盤子移到目標竿子。
將原來上面的盤子移到目標竿子。

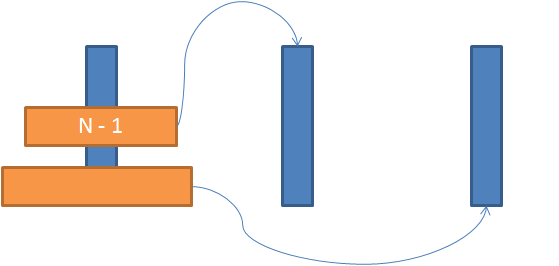
而當盤子 N 個的時候，其實也是依照同樣的邏輯進行即可，但上面 N - 1 個盤子要如何移到暫時擺放的竿子，這時候我們用遞迴的方式交給下一次呼叫自己去處理。

虛擬碼

function move(disks, from, to)
	if disks == 1
		自訂的移動動作
	else
		move(disks - 1, from, 另一竿子)
		move(1, from, to)
		move(disks - 1, 另一竿子, to)
	end if
end function

語法

這邊簡單將竿子用 1, 2, 3 編號

C#

static void Move(int disks, int from, int to)
{
    if (disks == 1)
    {
        Console.WriteLine("Move from {0} to {1}", from, to);
        return;
    }

    int relay = 6 - from - to;
    Move(disks - 1, from, relay);
    Move(1, from, to);
    Move(disks - 1, relay, to);
}

Java

public static void Move(int disks, int from, int to)
{
    if(disks == 1)
    {
        System.out.println("Move from " + from + " to " + to);
        return;
    }

    int relay = 6 - from - to;
    Move(disks - 1, from, relay);
    Move(1, from, to);
    Move(disks - 1, relay, to);
}

C++

void move(int disks, int from, int to)
{
    if(disks == 1)
    {
        cout << "Move from " << from << " to " << to << endl;
        return;
    }
    int relay = 6 - from - to;
    move(disks - 1, from, relay);
    move(1, from, to);
    move(disks - 1, relay, to);
}