計算 1 到 N 總和 (1 + 2 + 3 +...+ N)

題目

計算 1 到 N 總和 (1 + 2 + 3 +…+ N)
Sum the Integers from 1 to N.

這題看似很簡單，其實真的很簡單，只是可能會有不同要求。一般直覺會使用迴圈解，不過有時候也會要求遞迴解，考你簡單遞迴觀念。

int sum(int n)
{
    int sum = 0;
    for (int i = 1; i <= n; ++i)
        sum += i;
    return sum;
}

int sum(int n)
{
    if (n < 1)
        return 0;
    return n + sum(n - 1);
}

然後不論是迴圈還是遞迴解，都是 O(n) 的時間複雜度，有時候還會要求寫出O(1)的版本，這時候就要拿出數學的思考邏輯了，這沒記錯的話應該是高中數學的範圍。公式如下：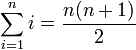

寫成程式

int sum(int n)
{
    return n * (n + 1) / 2;
}

推導參考維基百科。