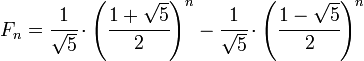簡介

費波那西數列 (Fibonacci)，又稱費氏數列、黃金分割數列等很多譯名，由西方的數學家費波那西使用兔子問題來描述這個數列，以下引用 Wiki：

  1. 第一個月初有一對剛誕生的兔子
  2. 第二個月之後(第三個月初)牠們可以生育
  3. 每月每對可生育的兔子會誕生下一對新兔子
  4. 兔子永不死去

使用數學式來表達的話如下：

1
2
3
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2)

列出前20個數值

F0F1F2F3F4F5F6F7F8F9F10F11F12F13F14F15F16F17F18F19F20
011235813213455891442333776109871597258441816765

演算法

數學法

解法有很多種，可以直接套數學公式，推導過程可參考 Wiki，公式如下：
費波那西數列公式

以程式設計的角度來看，一般使用迭代法、Divide and Conquery 和動態規劃 (Dynamic Programming) 的方式來解。

迭代法

由於每次新的問題的答案來自於前兩個問題，所以每次運算都保留前兩次的資料即可。

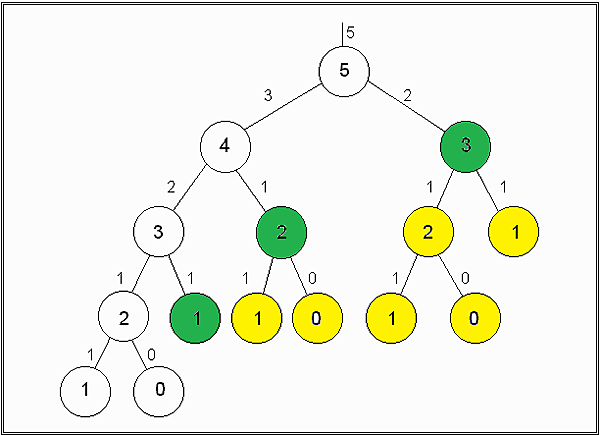
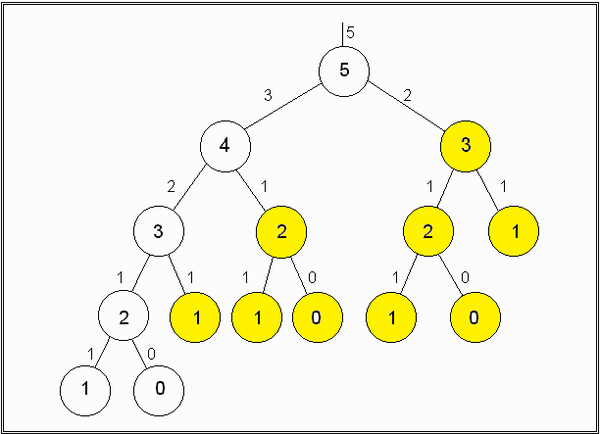
Divide and Conquery

一般最容易思考的解法是使用遞迴解，然而如同在 Divide and Conquer 和動態規劃兩篇文章中所說，Divide and Conquer 其實並不適用在此一問題，如下圖所示：
費波那西數列 Dynamic Programming

使用 Divide and Conquer 會重覆計算綠色和黃色的部分，造成效能大幅下降。

動態規劃

使用遞迴的動態規劃則可以記錄過計算過的部分，在綠色的部分會因為有 Cache 資料而不必計算，也不會在往下遞迴；另外也可以使用迴圈解的動態規劃，在思路上並不複雜，而且也減少 Function call 的消耗。

分析

時間複雜度

  • 迭代法：O(n)
  • 遞迴法：O(2^n)

虛擬碼

Divide and Conquery

1
2
3
4
5
6
7
8
function Fibonacci(n)
	if n == 0
		return 0
	if n == 1
		return 1
	end if
	return Fibonacci(n - 1) + Fibonacci(n - 2)
end function

動態規劃

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var map // cache of fibonacci
function Fibonacci(n)
	var value = map[n]
	if value == null
		if n == 0
			value = 0
		else if n == 1
			value = 1
		else
			value = Fibonacci(n - 1) + Fibonacci(n - 2)
		end if
		map[n] = value
	end if
	return value
end function

或 n=0 和 n=1 的先放入 Cache 中

1
2
3
4
5
6
7
8
9
var map // cache of fibonacci
map[0] = 0
map[1] = 1
function Fibonacci(n)
	if map[n] == null
		map[n] = Fibonacci(n - 1) + Fibonacci(n - 2)
	end if
	return map[n]
end function

語法

C#

數學法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Fibonacci
{
    class Mathematics
    {
        static double A = Math.Sqrt(5) / 5;
        static double B = (1 + Math.Sqrt(5)) / 2;
        static double C = (1 - Math.Sqrt(5)) / 2;
        public static long Fibonacci(int n)
        {
            return (long)(A * (Math.Pow(B, n) - Math.Pow(C, n)));
        }
    }
}

迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Fibonacci
{
    class Iterative
    {
        public static long Fibonacci(int n)
        {
            long v1 = 0;
            long v2 = 1;
            long result = n;
            for (int i = 2; i <= n; ++i)
            {
                result = v2 + v1;
                v1 = v2;
                v2 = result;
            }
            return result;
        }
    }
}

Divide and Conquery

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Fibonacci
{
    class DivideAndConquer
    {
        public static long Fibonacci(int n)
        {
            if (n == 0)
                return 0;
            if (n == 1)
                return 1;
            return Fibonacci(n - 1) + Fibonacci(n - 2);
        }
    }
}

動態規劃 - 遞迴解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Fibonacci
{
    class DynamicProgramming
    {
        static Dictionary<int, long> map = new Dictionary<int, long>() { { 0, 0 }, { 1, 1 } };
        public static long Fibonacci(int n)
        {
            if (map.ContainsKey(n))
                return map[n];
            return map[n] = Fibonacci(n - 1) + Fibonacci(n - 2);
        }
    }
}

動態規劃 - 迴圈解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Fibonacci
{
    class IterativeDynamicProgramming
    {
        public static long Fibonacci(int n)
        {
            Dictionary<int, long> map = new Dictionary<int, long>() { { 0, 0 }, { 1, 1 } };
            for (int i = 2; i <= n; ++i)
                map[i] = map[i - 1] + map[i - 2];
            return map[n];
        }
    }
}

Java

數學法

1
2
3
4
5
6
7
8
9
public class Mathematics {
    static double A = Math.sqrt(5) / 5;
    static double B = (1 + Math.sqrt(5)) / 2;
    static double C = (1 - Math.sqrt(5)) / 2;
    public static long Fibonacci(int n)
    {
        return (long)(A * (Math.pow(B, n) - Math.pow(C, n)));
    }
}

迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Iterative {
    public static long Fibonacci(int n)
    {
        long v1 = 0;
        long v2 = 1;
        long result = n;
        for (int i = 2; i <= n; ++i)
        {
            result = v2 + v1;
            v1 = v2;
            v2 = result;
        }
        return result;
    }
}

Divide and Conquery

1
2
3
4
5
6
7
8
9
10
public class DivideAndConquer {
    public static long Fibonacci(int n)
    {
        if (n == 0)
            return 0;
        if (n == 1)
            return 1;
        return Fibonacci(n - 1) + Fibonacci(n - 2);
    }
}

動態規劃-遞迴解

1
2
3
4
5
6
7
8
9
10
11
12
13
import java.util.HashMap;
import java.util.Map;

public class DynamicProgramming {
    static Map<Integer, Long> map = new HashMap<Integer, Long>() {{ put(0, 0L); put(1, 1L); }};
    public static long Fibonacci(int n)
    {
        if (map.containsKey(n))
            return map.get(n);
        map.put(n, Fibonacci(n - 1) + Fibonacci(n - 2));
        return map.get(n);
    }
}

動態規劃 - 迴圈解

1
2
3
4
5
6
7
8
9
10
11
12
13
import java.util.HashMap;
import java.util.Map;

public class IterativeDynamicProgramming {
    public static long Fibonacci(int n)
    {
        Map<Integer, Long> map = new HashMap<Integer, Long>() {{ put(0, 0L); put(1, 1L); }};

        for (int i = 2; i <= n; ++i)
            map.put(i, map.get(i - 1) + map.get(i - 2));
        return map.get(n);
    }
}

C++

數學法

Mathematics.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#ifndef MATHEMATICS_H
#define MATHEMATICS_H

#include <cmath>

class Mathematics
{
    public:
        static long Fibonacci(int n);
    protected:
    private:
        static double A;
        static double B;
        static double C;
};

#endif // MATHEMATICS_H

Mathematics.cpp

1
2
3
4
5
6
7
8
9
#include "Mathematics.h"

double Mathematics::A = sqrt(5) / 5;
double Mathematics::B = (1 + sqrt(5)) / 2;
double Mathematics::C = (1 - sqrt(5)) / 2;
long Mathematics::Fibonacci(int n)
{
    return (long)(A * (pow(B, n) - pow(C, n)));
}

迭代法

Iterative.h

1
2
3
4
5
6
7
8
9
10
11
12
13
#ifndef ITERATIVE_H
#define ITERATIVE_H


class Iterative
{
    public:
        static long Fibonacci(int n);
    protected:
    private:
};

#endif // ITERATIVE_H

Iterative.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include "Iterative.h"

long Iterative::Fibonacci(int n)
{
    long v1 = 0;
    long v2 = 1;
    long result = n;
    for (int i = 2; i <= n; ++i)
    {
        result = v2 + v1;
        v1 = v2;
        v2 = result;
    }
    return result;
}

Divide and Conquery

DivideAndConquer.h

1
2
3
4
5
6
7
8
9
10
11
12
13
#ifndef DIVIDEANDCONQUER_H
#define DIVIDEANDCONQUER_H


class DivideAndConquer
{
    public:
        static long Fibonacci(int n);
    protected:
    private:
};

#endif // DIVIDEANDCONQUER_H

DivideAndConquer.cpp

1
2
3
4
5
6
7
8
9
10
#include "DivideAndConquer.h"

long DivideAndConquer::Fibonacci(int n)
{
    if (n == 0)
        return 0;
    if (n == 1)
        return 1;
    return Fibonacci(n - 1) + Fibonacci(n - 2);
}

動態規劃 - 遞迴解

DynamicProgramming.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#ifndef DYNAMICPROGRAMMING_H
#define DYNAMICPROGRAMMING_H

#include <map>

using namespace std;

class DynamicProgramming
{
    public:
        static long Fibonacci(int n);
    protected:
    private:
        static pair<int, int> init[];
        static map<int, long> m;
};

#endif // DYNAMICPROGRAMMING_H

DynamicProgramming.cpp

1
2
3
4
5
6
7
8
9
10
#include "DynamicProgramming.h"

pair<int, int> DynamicProgramming::init[] = { make_pair(0, 0), make_pair(1, 1) };
map<int, long> DynamicProgramming::m(DynamicProgramming::init, DynamicProgramming::init + 2);
long DynamicProgramming::Fibonacci(int n)
{
    if (DynamicProgramming::m.count(n) == 1)
        return DynamicProgramming::m[n];
    return DynamicProgramming::m[n] = DynamicProgramming::Fibonacci(n - 1) + DynamicProgramming::Fibonacci(n - 2);
}

動態規劃 - 迴圈解

IterativeDynamicProgramming.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#ifndef ITERATIVEDYNAMICPROGRAMMING_H
#define ITERATIVEDYNAMICPROGRAMMING_H

#include <map>

using namespace std;

class IterativeDynamicProgramming
{
    public:
        static long Fibonacci(int n);
    protected:
    private:
};

#endif // ITERATIVEDYNAMICPROGRAMMING_H

IterativeDynamicProgramming.cpp

1
2
3
4
5
6
7
8
9
10
#include "IterativeDynamicProgramming.h"

long IterativeDynamicProgramming::Fibonacci(int n)
{
    pair<int, int> init[] = { make_pair(0, 0), make_pair(1, 1) };
    map<int, long> map(init, init + 2);
    for (int i = 2; i <= n; ++i)
        map[i] = map[i - 1] + map[i - 2];
    return map[n];
}

N=100 實測

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
C#
Mathematics: 4ms
Iterative: 4ms
IterativeDynamicProgramming: 10ms
DynamicProgramming: 12ms

Java
Mathematics: 30-40ms
Iterative: 30-40ms
IterativeDynamicProgramming: 30-40ms
DynamicProgramming: 30-40ms

C++
Mathematics: 0-10ms
Iterative: 0-2ms
IterativeDynamicProgramming: 0-2ms
DynamicProgramming: 0-10ms

延伸閱讀

動態規劃 (Dynamic Programming)
分治法 (Divide and conquer)