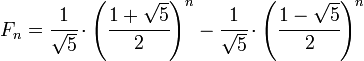簡介

Dynamic Programming 中文譯作動態規劃，動態規劃類似 Divide and Conquer，一個問題的答案來相依於子問題，常用來解決最佳解的問題。與 Divide and Conquer 不同的地方在於，動態規劃多使用了 memoization 的機制，將處理過的子問題答案記錄下來，避免重複計算，因此在子問題重疊的時候應該使用動態規劃；Divide and Conquer 通常使用遞迴 (Top-Down) 來處理，有時轉成迴圈 (Bottom-up) 來解並不容易，故使用動態規劃則可以解決重覆計算並保留遞迴思考的優點。

同樣拿費波那西數列 (Fibonacci) 為例子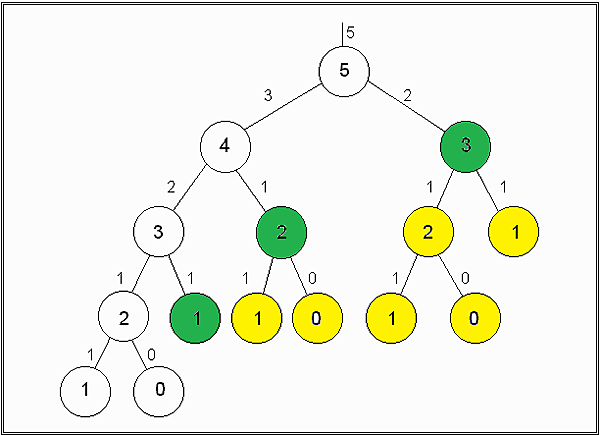
Dynamic Programming

使用 Divide and Conquer 的寫法如下：

1
2
3
4
5
6
7
8
function Fibonacci(n)
	if n == 0
		return 0
	if n == 1
		return 1
	end if
	return Fibonacci(n - 1) + Fibonacci(n - 2)
end function

如同之前在 Divide and conquer 一文中所說，會重覆計算黃色和綠色的部分，而改用動態規劃寫法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var map // cache of fibonacci
function Fibonacci(n)
	var value = map[n]
	if value == null
		if n == 0
			value = 0
		else if n == 1
			value = 1
		else
			value = Fibonacci(n - 1) + Fibonacci(n - 2)
		end if
		map[n] = value
	end if
	return value
end function

結果在綠色部分就會因為有 Cache 資料而不必計算，也不會在往下遞迴，而達到增進效能的目的。另外也可以直接將 n=0 和 n=1 的資料事先放入 Cache 中：

1
2
3
4
5
6
7
8
9
var map // cache of fibonacci
map[0] = 0
map[1] = 1
function Fibonacci(n)
	if map[n] == null
		map[n] = Fibonacci(n - 1) + Fibonacci(n - 2)
	end if
	return map[n]
end function

相關範例