小殘的程式光廊

拍攝時間：2012 年 10 月 8 日 今天又來到了陽明山，不過走的點不一樣，這次是在陽明公園這邊下車，從陽明公園往大屯瀑布行走。 地址：112 台北市北投區湖山路二段 26 號 電話：0228832130 10 月這個季節來陽明山似乎看不到甚麼特別的花季，就看看綠色的樹木吧 剛進來不久就看到一隻松鼠 他在吃甚麼呢？其實是剛剛有放一塊餅乾在地上，他就跳下來拿去吃了 夏秋交際的日子，開的花就這麼多了 原來陽明山的名字是來自王陽明的陽明兩字，陽明山以前叫做草山 公園裡面有些小河和池塘 辛亥光復樓，裡面有賣些特產和紀念品 在辛亥光復樓旁邊的大樹，不過流動廁所和汽車在後面倒是挺搶鏡的 繼續往前走來到了一個木棚步道，看起來還不錯 來到了觀景台，可以看到另一邊的山，下方都被樹擋住了，視野似乎不是很好 觀景台旁的山坡也有一些小花 來到大屯瀑布，大部分的人都在這休息和運動 從旁邊可以走到上一張照片的上面的橋梁，往下照一張 離開瀑布區後來到了停車場附近的花鐘，這邊沒有比較好的視角可以從上往下照，倒是沒注意時間有沒有準 在停車場這邊有開一些小吃店，午餐就在這邊解決，價格並沒有因為是觀光景點而變貴 ...

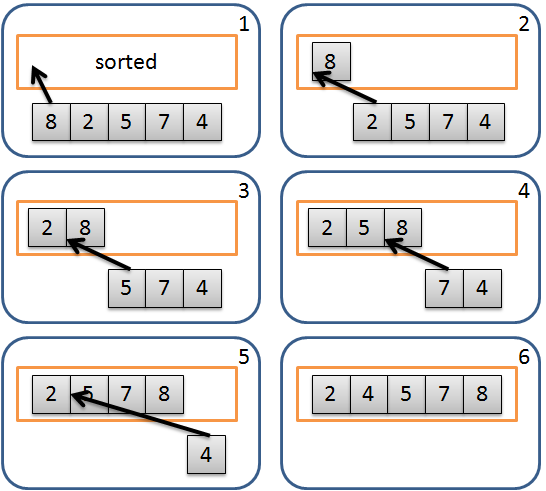
簡介排序 (Sorting) 演算法是常用到的一種演算法，顧名思義他是用來將資料依據特定的規則做排序後輸出；既然稱為排序就會有一個比較順序的依據，例如數字就比較數值大小、字串則依 ASCII 字母順序或者物件會有自定義的規則。一般沒有特別指定的話，輸出是以遞增排序為準。 穩定排序排序演算法分為穩定 (Stable) 和不穩定 (Unstable) 兩種，是指當資料中有相等數值的兩元素，經過排序之後是否能夠保持原有的相對位置，例如： 1(猴子, 智商60) (丁丁, 智商20) (拉拉, 智商20) (路人甲, 智商90) 將這些資料依據智商來排序，會發現智商 20 的有兩位，因此我們可能得到以下兩種情況 12(丁丁, 智商20) (拉拉, 智商20) (猴子, 智商60) (路人甲, 智商90)(拉拉, 智商20) (丁丁, 智商20) (猴子, 智商60) (路人甲, 智商90) 第一種情況丁丁和拉拉與原始的相對位置一致 (丁丁在前)，能夠總是維持相對位置的排序法我們稱之為穩定排序，反之則稱為不穩定排序，不能確保相對位置與原來一樣 (但是也有可能一樣)。 如果是純數字的排序基本上是 ...

資訊 路徑：Tournament \ 1-16 \ 2 - Inv 2001 Semi A+B \ Tothello 分數：500 題目程式介面12345Class Name: TothelloMethod Name: bestMoveParameters: String[], String[], StringReturns: intMethod signature (be sure your method is public): int bestMove(String[] redPieces, String[] blackPieces, String whoseTurn); 說明Tothello 是一個 Othello 遊戲的修改版，Othello 是一種兩人玩的遊戲，一方使用紅色的棋子，一方使用黑色的棋子，輪流在一個 8x8 大小的棋盤上下棋。當一方下棋之後，如果有將對方的棋子兩端包夾起來，對方的棋子就會變成自己的棋子；而若有棋子變成自己的棋子後，又產生其他的包夾，則又可以變成自己的棋子，直到沒有任何包夾。另外自己的回合的時候，也可以選擇 Pass 不下棋。 現在請實作一個程 ...

簡介連結串列 (Linked List 或稱鏈結串列) 是串列 (List) 的一種，是一種常見的資料結構，利用這個資料結構也能進一步實作出其他的資料結構，例如堆疊 (Stack) 和佇列 (Queue) 等。 它的特性是能夠不使用連續的記憶體空間的情況下，能夠保有並使用一份連續的資料；相對來看，陣列則需要使用連續的記憶體空間。 他的的實作方式是每個節點除了記錄資料之外，還使用額外的指標指向下一個節點，將節點以此方式串連起來形成一個連結串列。 由以上的說明可以知道，使用連結串列的優點如下： 不需使用連續記憶體空間，不需事先指定串列大小。 能夠容易的修改指標，插入或移除節點。 但也有缺點如下： 使用額外的記憶體空間紀錄節點指標。 無法快速索引到某個節點，必須迭代搜索。 此資料結構可以實作的操作變化相當多，這裡實作以下幾種操作： getFirst：取得第一個節點。 getLast：取得最後一個節點。 addFirst：加入節點在最前面。 addLast：加入節點到最後。 addBefore：加入節點在某節點之前。 addAfter：加入節點在某節點之後。 removeFirst： ...

簡介佇列 (Queue) 中文也翻作隊列，顧名思義是一種像排隊一樣的概念，以生活中的情況為例如下圖 人們一個接一個的從隊伍後面加入排隊，而窗口的服務人員則從最前面的民眾一個接一個處理事務；當然現實生活是會有中途離開的人，而在程式世界裡面一般情況是不會有。 在這個模式下我們可以知道他是一種先進先出 (First-In-First-Out, FIFO) 的排程，而在此資料結構中至少會實作兩個操作： enqueue：將資料放入佇列尾端。(註：C++ 中用 push、Java 用 offer、也有 add 等不同的用字) dequeue：取出佇列前端之資料。(註：C++ 中用 pop、Java 用 poll、也有 remove 等不同的用字) 有時候也會多實作一些額外的操作以方便使用，例如： peek：看佇列前端的資料而不取出。(註：也有 front 等不同的用字) size：取得佇列的數目。 在實作上一般使用連結串列 (LinkedList) 來實作，使用陣列同樣可以達成，但較為複雜： 連結串列用指標將資料串起來，將新的東西不斷接在最後面，而取出時則移除最前面的東西即可。由於加入和移 ...

簡介堆疊 (Stack) 是資料結構的一種，是一種很基本常見的資料結構，首先利用現實生活中的例子來說明，如下圖 假設你有一些書把他們疊起來，一層一層的往上疊，所以每次新的書本會放在最上面，而當想要拿取書本的時候，也是從最上面的開始拿。當然現實生活會有可能從中間抽出書本，不過在程式中是不可以的，在程式世界下圖會更貼切。 所以他是一種後進先出 (Last-In-First-Out, LIFO) 的排程，而在此資料結構中至少會實作兩個操作： push：將資料放入堆疊頂端 pop：取出堆疊頂端之資料 有時候也會多實作一些額外的操作以方便使用，例如： peek：看堆疊頂端的資料而不取出。。(註：也有 top 等不同的用字) size：取得堆疊的數目。 在實作上一般可以使用陣列或連結串列 (LinkedList) 兩種方式來實作： 陣列堆疊建立時即建立一個陣列，並使用一個索引來記錄目前所指到的位址，新增或移除資料時，同步修改索引位址；如果有實作堆疊數目的功能時，這數字正好可做為此索引之用。優點是不用處理指標鏈結建立與移除，缺點是容量超過陣列大小時需要額外處理。 連結串列用指標將資料串起來， ...

拍攝時間：2012 年 7 月 1 日 這天用了下午的時間帶朋友去新竹的一些小景點逛逛，首先來到靜心湖，之前住在這附近住了一年都不知道這裡有個湖，藏身於園區附近的一個景點。 從金山街出發的話，可以從星巴克對面的小路過去，一直到新竹家扶中心旁邊就可以進入了。 靜心湖 進入靜心湖之後，我們先從仿古代庭院造景的地方穿過，來到蓮花池。 正值夏天，可以看到一些蓮花綻放。 也有很多蓮藕。 仿古代的庭院造景，不能看太仔細，不然就會穿幫(都不是木造)。 旁邊有一棟外觀看起來別致的建築，其實這是廁所。 穿過庭院之後，有個太極的雕像造景，有很多民眾會來這邊運動，不知道有沒有打太極拳就是了。 在湖的正中央有一個小島，有座橋可以通過去。 這座大廈相當的搶鏡，上次來還沒蓋好，現在好像完成了。 我們從這座橋走到了小島。 七月了，在這座小島上竟然還有櫻花？ 走近一看，原來是假的，用燈泡做成的櫻花，不知道晚上會不會亮。 新竹公園新竹公園這一帶集合了玻璃工藝博物館、假日花市、動物園和孔廟等等景點。 這裡也有一小片湖，可以從照片中的橋穿過。 這裡有不少的鳥類和水中生物棲息，一隻白鷺鷥停在灑水器上。 這裡也來過很多次 ...

簡介先來描述一下問題，這裡以下樓梯為例： 有一個人下樓梯，一次可以走一階或兩階，假設總共有N階樓梯，共有幾總走法？例如 N = 3，他可以走 1 + 1 + 1 、1 + 2 或 2 + 1 三種走法。 實做一個程式能夠輸入 N，能回傳共有幾總走法。 演算法這個問題直接使用 Bottom-Up 可能不容易思考，所以我們先利用遞迴的 Top-Down 思考邏輯來想這個問題，結果我們很容易就可以這樣想： 第N階的走法相當於在 N - 1 階的時候走一階過來，或者在 N - 2 階的時候走兩階過來；換句話說，就是第N階的走法等於N - 1階的走法加上N - 2階的走法。 所以我們就可以寫出遞迴式： 123F(N) = F(N - 1) + F(N - 2)F(1) = 1F(2) = 2 列出來的式子和費波那西數列 (Fibonacci) 還蠻像的，我們可以用不同的方式去實做解這問題，這問題較適合用動態規劃 (Dynamic Programming) 去解，直接用 Divide and Conquer 會重覆計算子問題。由於此問題和費波那西數列相當相似，這邊只簡單實做迭代法和動態規 ...

常見考題包含了基礎的演算法和資料結構，以及一些其他類型的程式實作考題。 演算法 分治法 (Divide and conquer) 二元搜索法 (Binary Search) 動態規劃 (Dynamic Programming) 費波那西數列 (Fibonacci) 上下樓梯問題 & (籃球) 得分問題 最大子序列 (Maximum Subarray) 排序演算法 (Sorting) 資料結構 連結串列 (LinkedList) 堆疊 (Stack) 佇列 (Queue) 其他考古題 不使用暫存變數交換兩個變數 (Swap two variables without using a temporary variable) 計算 1 + 2 + 3 + … + N 的總和 (Sum the Integers from 1 to N)可以思考不同的解法，例如： 使用遞迴 比 O(n) 時間複雜度更快的方法 計算1 * 2 + 2 * 3 + … + (N - 1) * N的總和 (Write a function to calculate 1 * 2 + 2 * 3 ...

題目未排序的 n 個連續整數中少了一個，試著找到最快的方法算出少了哪一個。例如：3, 6, 9, 7, 8, 4，連續整數範圍為 3-9，少了 5。How to find the missing integer in an array. 說明這個題目我們直覺得可以使用 Hashtable 的方式來判斷哪些數字出現過，但是這樣題目就太簡單了，所以一般會再有一個額外的限制：空間複雜度為 O(1)。 所以在不使用 Hashtable 的情況下，我們只能用數學的方式去求解，此等差數列正好為梯形公式：(上底 + 下底) * 高 / 2。 接著利用公式的理論總和減去實際總和就是缺少的數字，以上面的例子為例： 123(3 + 9) * 7 / 2 = 423 + 6 + 9 + 7 + 8 + 4 = 3742 - 37 = 5 解法1234567891011121314static int Find(int[] array){ int max = array[0]; int min = array[0]; int sum = 0; for (int i ...