樹的走訪 (Tree Traversal)
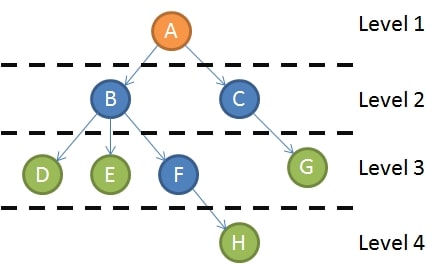
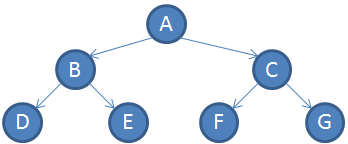
簡介透過一些演算法能夠對樹狀結構的節點進行逐一的訪問,可以應用在搜索、序列化或其他的用途上。依據走訪的方式,大致上可分為以下兩大類: 深度優先 (Depth-first)深度優先又分為三種走訪方式,而一般樹和二元樹以下分開來討論: 一般樹 前序 (Pre-order) 訪問根節點 訪問所有子樹 上圖的走訪順序為:ABDEFHCG 中序 (In-order) 訪問第一個子樹 訪問根節點 訪問其他子樹 上圖的走訪順序為:DBEHFAGC 事實上一般樹的情況下,中序走訪並不實用。 後序 (Post-order) 訪問所有子樹 訪問根節點 上圖的走訪順序為:DEHFBGCA 二元樹 前序 (Pre-order) 訪問根節點 訪問左子樹 訪問右子樹 上圖的走訪順序為:ABDECFG 中序 (In-order) 訪問左子樹 訪問根節點 訪問右子樹 上圖的走訪順序為:DBEAFCG 後序 (Post-order) 訪問左子樹 訪問右子樹 訪問根節點 上圖的走訪順序為:DEBFGCA 廣度優先 (Breadth-first)廣度優先又可以稱為 Level-order,將每一 ...
資料結構 - 一般樹轉二元樹
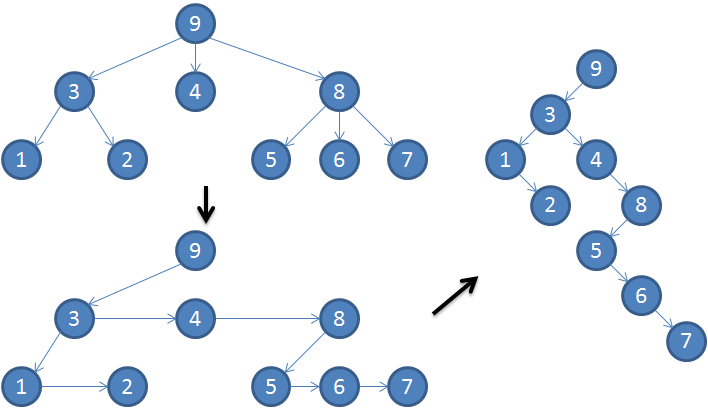
簡介在樹狀結構中我們可能會使用陣列或指標來表示子節點,然而許多的陣列或指標並沒有真的利用到,造成記憶體上的浪費。透過特定的儲存方式,能夠將各種樹都轉換成二元樹,就能有效解決這個問題。轉換的規則如下: 原節點的第一個子節點轉成二元樹中的左子節點 。 原節點的下一個兄弟節點轉成二元樹中的右子節點。 從圖形的角度來看也可以這樣說: 原節點的第一個指標指向第一個子節點。 原節點的第二個指標指向下一個兄弟節點。 轉換過程以下面這張圖為例: 左上角的圖表示原來的一般樹,從圖形的角度並以節點3為例,透過規則1將節點3的第一個指標指向第一個子節點,第一個節點我們簡單取最左邊的節點,為節點 1;透過規則 2 將節點 3 的第二個指標指向下一個兄弟節點,為節點 4。 其他以此類推,接著我們可以得到左下角的圖形,與原來的規則做對應我們可以知道,第一個指標指的就是二元樹的左子節點,第二個指標就是右子節點,所以依據左右子節點的位置重新調整圖形,最後可以得到右邊的徒刑,也就是轉換成二元樹的結果。 LCRS Tree從上面的轉換結果,我們可以知道這個二元樹的左子節點代表的是原來的第一個子節點,右子節點代表下 ...
資料結構 - 二元搜索樹 (Binary Search Tree)
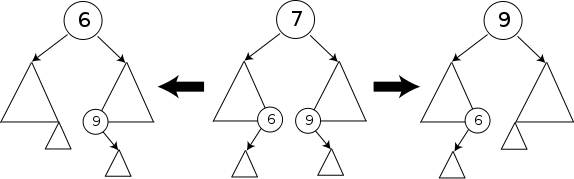
簡介二元搜索樹 (Binary Search Tree) 是基於二元樹的一種延伸,二元搜索樹的應用範圍很廣,可以利用在搜索、排序和提供資料集合基本結構,發展其他資料結構,所以也是重要的資料結構之一。 定義定義除了繼承二元樹的定義外,二元搜索樹本身也有額外的定義,但可能會看到幾種不同的說法,而較多數人使用的定義如下: 左子樹不為空,則左子樹的所有節點的鍵值 (Key) 小於根節點的鍵值。 右子樹不為空,則右子樹的所有節點的鍵值 (Key) 大於根節點的鍵值。 左右子樹也都是二元搜索樹。 節點不會有重複的鍵值。 這個定義是樹中的節點都具有 Key-value pair 情況,有時候可能會其他變化: 沒有鍵值,而用值 (Value) 來比較。 允許重複的資料,此時會出現等於的情況,則將定義 1. 改成小於等於或者定義 2. 改成大於等於。 以下為示意圖: 實作不同類型的樹會有不同的介面,原始版本通常會實作以下介面: add: 加入資料。(或 insert) remove: 移除資料。(或 delete) containsKey: 判斷是否包含鍵值。 get: 取出資料。 無鍵值的 ...
資料結構 - 二元樹 (Binary Tree)
簡介二元樹 (Binary Tree) 是資料結構中樹狀結構的一種,也是常使用的一種資料結構,很多其他的樹種也是基於二元樹發展出來,所以是很重要的一種資料結構。 定義二元樹顧名思義是指每個節點都最多只能有兩個分支,所以會看起來這樣: 而比較嚴謹的定義如下: 每個節點最多有兩個子節點。 子節點有左右之分。 當然原來樹的定義也是要繼承下來。 在二元樹中也定義了一些專有名詞,解釋如下: 完滿二元樹 (Full Binary Tree)或翻譯滿二元樹,每個節點有 0 或 2 個子節點。也稱作嚴格二元樹 (Strictly Binary Tree)、正規二元樹 (Proper Binary Tree) 或 2-tree。範例如下: 大多數的中文資料對完滿二元樹的定義相當於英文的完美二元樹。 完全二元樹 (Complete Binary Tree)除了最後一階層之外的階層都必須填滿,而最後一階層的節點必須由左至右填入。範例如下: 完美二元樹 (Perfect Binary Tree)同時滿足完滿二元樹的條件,並且所有的葉節點都在同一個階層。範例如下: 在這個定義下可以得知,完美二元樹也必定是完 ...
資料結構 - 樹 (Tree)
簡介樹 (Tree) 是一種常見的資料結構,他是一種階層式 (Hierarchical) 的資料集合,我們就先來看看下面這棵樹: 我們觀察這棵樹之後可以發現他由某些東西組成,包含樹葉、樹枝和樹幹;同樣地,在程式世界裡有著類似的對應,樹的最開始會有一個根節點,就像樹的樹根一樣,所有的資料都是由這裡開始發展,接著會有一些其他的節點,有些節點可能在最末端,稱之為葉節點,就像樹的樹葉一樣,其他的節點則像樹的樹枝一樣。 不過在程式世界裡面,我們習慣把根節點放在最上面,而在我們生活中其實也很常使用,像是組織圖: 上圖的區長為根節點,最下面的各單位則為葉節點。 定義在數學的圖論和資料結構所提到的樹其實有些差異,在這裡先說明兩者的不同,數學中對樹的定義這裡簡化如下: 圖中任兩點存在一條路經相通,但不存在環 (Cycle)。 不過在資料結構裡面所說的樹,指的是數學裡的有根樹 (Rooted tree),定義如下: 有一個特殊節點為根節點的樹。 在資料結構中的實作會有父節點和子節點的分別,所以可以進一步的定義: 樹存在一個為根節點,根節點沒有父節點 (不可以有迴圈)。 每個節點只有一個父節點 ( ...
資料結構 - 連結串列 (Linked List)
簡介連結串列 (Linked List 或稱鏈結串列) 是串列 (List) 的一種,是一種常見的資料結構,利用這個資料結構也能進一步實作出其他的資料結構,例如堆疊 (Stack) 和佇列 (Queue) 等。 它的特性是能夠不使用連續的記憶體空間的情況下,能夠保有並使用一份連續的資料;相對來看,陣列則需要使用連續的記憶體空間。 他的的實作方式是每個節點除了記錄資料之外,還使用額外的指標指向下一個節點,將節點以此方式串連起來形成一個連結串列。 由以上的說明可以知道,使用連結串列的優點如下: 不需使用連續記憶體空間,不需事先指定串列大小。 能夠容易的修改指標,插入或移除節點。 但也有缺點如下: 使用額外的記憶體空間紀錄節點指標。 無法快速索引到某個節點,必須迭代搜索。 此資料結構可以實作的操作變化相當多,這裡實作以下幾種操作: getFirst:取得第一個節點。 getLast:取得最後一個節點。 addFirst:加入節點在最前面。 addLast:加入節點到最後。 addBefore:加入節點在某節點之前。 addAfter:加入節點在某節點之後。 removeFirst: ...
資料結構 - 佇列 (Queue)
簡介佇列 (Queue) 中文也翻作隊列,顧名思義是一種像排隊一樣的概念,以生活中的情況為例如下圖 人們一個接一個的從隊伍後面加入排隊,而窗口的服務人員則從最前面的民眾一個接一個處理事務;當然現實生活是會有中途離開的人,而在程式世界裡面一般情況是不會有。 在這個模式下我們可以知道他是一種先進先出 (First-In-First-Out, FIFO) 的排程,而在此資料結構中至少會實作兩個操作: enqueue:將資料放入佇列尾端。(註:C++ 中用 push、Java 用 offer、也有 add 等不同的用字) dequeue:取出佇列前端之資料。(註:C++ 中用 pop、Java 用 poll、也有 remove 等不同的用字) 有時候也會多實作一些額外的操作以方便使用,例如: peek:看佇列前端的資料而不取出。(註:也有 front 等不同的用字) size:取得佇列的數目。 在實作上一般使用連結串列 (LinkedList) 來實作,使用陣列同樣可以達成,但較為複雜: 連結串列用指標將資料串起來,將新的東西不斷接在最後面,而取出時則移除最前面的東西即可。由於加入和移 ...
資料結構 - 堆疊 (Stack)
簡介堆疊 (Stack) 是資料結構的一種,是一種很基本常見的資料結構,首先利用現實生活中的例子來說明,如下圖 假設你有一些書把他們疊起來,一層一層的往上疊,所以每次新的書本會放在最上面,而當想要拿取書本的時候,也是從最上面的開始拿。當然現實生活會有可能從中間抽出書本,不過在程式中是不可以的,在程式世界下圖會更貼切。 所以他是一種後進先出 (Last-In-First-Out, LIFO) 的排程,而在此資料結構中至少會實作兩個操作: push:將資料放入堆疊頂端 pop:取出堆疊頂端之資料 有時候也會多實作一些額外的操作以方便使用,例如: peek:看堆疊頂端的資料而不取出。。(註:也有 top 等不同的用字) size:取得堆疊的數目。 在實作上一般可以使用陣列或連結串列 (LinkedList) 兩種方式來實作: 陣列堆疊建立時即建立一個陣列,並使用一個索引來記錄目前所指到的位址,新增或移除資料時,同步修改索引位址;如果有實作堆疊數目的功能時,這數字正好可做為此索引之用。優點是不用處理指標鏈結建立與移除,缺點是容量超過陣列大小時需要額外處理。 連結串列用指標將資料串起來, ...